Difference between revisions of "AY Honors/Math Skills III/Requirements"
Jomegat bot (talk | contribs) m (Protected "AY Honor Math Skills III Requirements": Bot: Protecting all pages from category .*/e[sn] ([Move=Allow only administrators] (indefinite) [Edit=Allow only administrators] (indefinite))) |
(Marked this version for translation) |
||
| Line 6: | Line 6: | ||
| − | <b>1. <section begin=req1 /><noinclude><translate></noinclude>Have the Math Skills II honor. | + | <b>1. <section begin=req1 /><noinclude><translate><!--T:1--> |
| + | </noinclude>Have the Math Skills II honor. | ||
<noinclude></translate></noinclude><section end=req1 /></b> | <noinclude></translate></noinclude><section end=req1 /></b> | ||
| − | <b>2. <section begin=req2 /><noinclude><translate></noinclude>Solve the following operations using the traditional algorithm: | + | <b>2. <section begin=req2 /><noinclude><translate><!--T:2--> |
| + | </noinclude>Solve the following operations using the traditional algorithm: | ||
<noinclude></translate></noinclude><section end=req2 /></b> | <noinclude></translate></noinclude><section end=req2 /></b> | ||
| − | :<b>a. <section begin=req2a /><noinclude><translate></noinclude>641 + 135 | + | :<b>a. <section begin=req2a /><noinclude><translate><!--T:3--> |
| + | </noinclude>641 + 135 | ||
<noinclude></translate></noinclude><section end=req2a /></b> | <noinclude></translate></noinclude><section end=req2a /></b> | ||
| − | :<b>b. <section begin=req2b /><noinclude><translate></noinclude>845 - 124 | + | :<b>b. <section begin=req2b /><noinclude><translate><!--T:4--> |
| + | </noinclude>845 - 124 | ||
<noinclude></translate></noinclude><section end=req2b /></b> | <noinclude></translate></noinclude><section end=req2b /></b> | ||
| − | :<b>c. <section begin=req2c /><noinclude><translate></noinclude>34 x 125 | + | :<b>c. <section begin=req2c /><noinclude><translate><!--T:5--> |
| + | </noinclude>34 x 125 | ||
<noinclude></translate></noinclude><section end=req2c /></b> | <noinclude></translate></noinclude><section end=req2c /></b> | ||
| − | :<b>d. <section begin=req2d /><noinclude><translate></noinclude>856 ÷ 24 | + | :<b>d. <section begin=req2d /><noinclude><translate><!--T:6--> |
| + | </noinclude>856 ÷ 24 | ||
<noinclude></translate></noinclude><section end=req2d /></b> | <noinclude></translate></noinclude><section end=req2d /></b> | ||
| − | <b>3. <section begin=req3 /><noinclude><translate></noinclude>Identify and classify the numerical sets. | + | <b>3. <section begin=req3 /><noinclude><translate><!--T:7--> |
| + | </noinclude>Identify and classify the numerical sets. | ||
<noinclude></translate></noinclude><section end=req3 /></b> | <noinclude></translate></noinclude><section end=req3 /></b> | ||
| − | <b>4. <section begin=req4 /><noinclude><translate></noinclude>Demonstrate the ability to solve the following equations: | + | <b>4. <section begin=req4 /><noinclude><translate><!--T:8--> |
| + | </noinclude>Demonstrate the ability to solve the following equations: | ||
<noinclude></translate></noinclude><section end=req4 /></b> | <noinclude></translate></noinclude><section end=req4 /></b> | ||
| − | :<b>a. <section begin=req4a /><noinclude><translate></noinclude>2x - 10 = -4x + 14 | + | :<b>a. <section begin=req4a /><noinclude><translate><!--T:9--> |
| + | </noinclude>2x - 10 = -4x + 14 | ||
<noinclude></translate></noinclude><section end=req4a /></b> | <noinclude></translate></noinclude><section end=req4a /></b> | ||
| − | :<b>b. <section begin=req4b /><noinclude><translate></noinclude>18x - 43 = 65 | + | :<b>b. <section begin=req4b /><noinclude><translate><!--T:10--> |
| + | </noinclude>18x - 43 = 65 | ||
<noinclude></translate></noinclude><section end=req4b /></b> | <noinclude></translate></noinclude><section end=req4b /></b> | ||
| − | :<b>c. <section begin=req4c /><noinclude><translate></noinclude>23x - 16 = 14 - 17x | + | :<b>c. <section begin=req4c /><noinclude><translate><!--T:11--> |
| + | </noinclude>23x - 16 = 14 - 17x | ||
<noinclude></translate></noinclude><section end=req4c /></b> | <noinclude></translate></noinclude><section end=req4c /></b> | ||
| − | :<b>d. <section begin=req4d /><noinclude><translate></noinclude>10y - 5(1 + y) = 3(2y - 2) - 20 | + | :<b>d. <section begin=req4d /><noinclude><translate><!--T:12--> |
| + | </noinclude>10y - 5(1 + y) = 3(2y - 2) - 20 | ||
<noinclude></translate></noinclude><section end=req4d /></b> | <noinclude></translate></noinclude><section end=req4d /></b> | ||
| − | :<b>e. <section begin=req4e /><noinclude><translate></noinclude>x(x + 4) + x(x + 2) = 2x² + 12 | + | :<b>e. <section begin=req4e /><noinclude><translate><!--T:13--> |
| + | </noinclude>x(x + 4) + x(x + 2) = 2x² + 12 | ||
<noinclude></translate></noinclude><section end=req4e /></b> | <noinclude></translate></noinclude><section end=req4e /></b> | ||
| − | :<b>f. <section begin=req4f /><noinclude><translate></noinclude>(x - 5) / 10 + (1 - 2x) / 5 = (3-x) / 4 | + | :<b>f. <section begin=req4f /><noinclude><translate><!--T:14--> |
| + | </noinclude>(x - 5) / 10 + (1 - 2x) / 5 = (3-x) / 4 | ||
<noinclude></translate></noinclude><section end=req4f /></b> | <noinclude></translate></noinclude><section end=req4f /></b> | ||
| − | :<b>g. <section begin=req4g /><noinclude><translate></noinclude>4x(x + 6) - x² = 5x² | + | :<b>g. <section begin=req4g /><noinclude><translate><!--T:15--> |
| + | </noinclude>4x(x + 6) - x² = 5x² | ||
<noinclude></translate></noinclude><section end=req4g /></b> | <noinclude></translate></noinclude><section end=req4g /></b> | ||
| − | <b>5. <section begin=req5 /><noinclude><translate></noinclude>Demonstrate the ability to solve the following products: | + | <b>5. <section begin=req5 /><noinclude><translate><!--T:16--> |
| + | </noinclude>Demonstrate the ability to solve the following products: | ||
<noinclude></translate></noinclude><section end=req5 /></b> | <noinclude></translate></noinclude><section end=req5 /></b> | ||
| − | :<b>a. <section begin=req5a /><noinclude><translate></noinclude>(x + 3y)² | + | :<b>a. <section begin=req5a /><noinclude><translate><!--T:17--> |
| + | </noinclude>(x + 3y)² | ||
<noinclude></translate></noinclude><section end=req5a /></b> | <noinclude></translate></noinclude><section end=req5a /></b> | ||
| − | :<b>b. <section begin=req5b /><noinclude><translate></noinclude>(a<sup>5</sup> + 2bc)² | + | :<b>b. <section begin=req5b /><noinclude><translate><!--T:18--> |
| + | </noinclude>(a<sup>5</sup> + 2bc)² | ||
<noinclude></translate></noinclude><section end=req5b /></b> | <noinclude></translate></noinclude><section end=req5b /></b> | ||
| − | :<b>c. <section begin=req5c /><noinclude><translate></noinclude>(3x + y²)² | + | :<b>c. <section begin=req5c /><noinclude><translate><!--T:19--> |
| + | </noinclude>(3x + y²)² | ||
<noinclude></translate></noinclude><section end=req5c /></b> | <noinclude></translate></noinclude><section end=req5c /></b> | ||
| − | :<b>d. <section begin=req5d /><noinclude><translate></noinclude>(1 + 5m)(1 - 5m) | + | :<b>d. <section begin=req5d /><noinclude><translate><!--T:20--> |
| + | </noinclude>(1 + 5m)(1 - 5m) | ||
<noinclude></translate></noinclude><section end=req5d /></b> | <noinclude></translate></noinclude><section end=req5d /></b> | ||
| − | :<b>e. <section begin=req5e /><noinclude><translate></noinclude>(ab - c)² | + | :<b>e. <section begin=req5e /><noinclude><translate><!--T:21--> |
| + | </noinclude>(ab - c)² | ||
<noinclude></translate></noinclude><section end=req5e /></b> | <noinclude></translate></noinclude><section end=req5e /></b> | ||
| − | :<b>f. <section begin=req5f /><noinclude><translate></noinclude>(m - 1)³ | + | :<b>f. <section begin=req5f /><noinclude><translate><!--T:22--> |
| + | </noinclude>(m - 1)³ | ||
<noinclude></translate></noinclude><section end=req5f /></b> | <noinclude></translate></noinclude><section end=req5f /></b> | ||
| − | :<b>g. <section begin=req5g /><noinclude><translate></noinclude>(a³ - b³) (a³ + b³) | + | :<b>g. <section begin=req5g /><noinclude><translate><!--T:23--> |
| + | </noinclude>(a³ - b³) (a³ + b³) | ||
<noinclude></translate></noinclude><section end=req5g /></b> | <noinclude></translate></noinclude><section end=req5g /></b> | ||
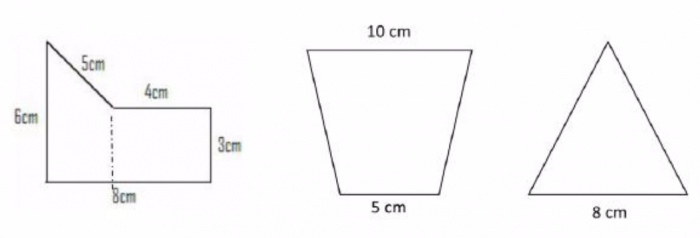
| − | <b>6. <section begin=req6 /><noinclude><translate></noinclude>Calculate the area of the following figures: | + | <b>6. <section begin=req6 /><noinclude><translate><!--T:24--> |
| + | </noinclude>Calculate the area of the following figures: | ||
[[File:Math Skills III figures.png|700px]] | [[File:Math Skills III figures.png|700px]] | ||
<noinclude></translate></noinclude><section end=req6 /></b> | <noinclude></translate></noinclude><section end=req6 /></b> | ||
| − | <b>7. <section begin=req7 /><noinclude><translate></noinclude>In the [[Adventist_Youth_Honors_Answer_Book/Recreation/Orienteering|Orienteering]] honor, the Pathfinder must have knowledge of angles to know how to use cartographic charts and to use a compass. Demonstrate the ability to convert angles to minutes, minutes to seconds, showing three practical examples. | + | <b>7. <section begin=req7 /><noinclude><translate><!--T:25--> |
| + | </noinclude>In the [[Adventist_Youth_Honors_Answer_Book/Recreation/Orienteering|Orienteering]] honor, the Pathfinder must have knowledge of angles to know how to use cartographic charts and to use a compass. Demonstrate the ability to convert angles to minutes, minutes to seconds, showing three practical examples. | ||
<noinclude></translate></noinclude><section end=req7 /></b> | <noinclude></translate></noinclude><section end=req7 /></b> | ||
| − | <b>8. <section begin=req8 /><noinclude><translate></noinclude>In the [[Adventist_Youth_Honors_Answer_Book/Recreation/Pioneering|Pioneering]] honor, we learned to build camp furniture, which has a whole mathematical relationship. Design and present some camp furniture where geometric shapes appear and classify each one. Cite three examples. | + | <b>8. <section begin=req8 /><noinclude><translate><!--T:26--> |
| + | </noinclude>In the [[Adventist_Youth_Honors_Answer_Book/Recreation/Pioneering|Pioneering]] honor, we learned to build camp furniture, which has a whole mathematical relationship. Design and present some camp furniture where geometric shapes appear and classify each one. Cite three examples. | ||
<noinclude></translate></noinclude><section end=req8 /></b> | <noinclude></translate></noinclude><section end=req8 /></b> | ||
| − | <b>9. <section begin=req9 /><noinclude><translate></noinclude>Present a poster showing ten practical examples of geometric figures used in a daily routine. It can be as cutouts, photos or design. | + | <b>9. <section begin=req9 /><noinclude><translate><!--T:27--> |
| + | </noinclude>Present a poster showing ten practical examples of geometric figures used in a daily routine. It can be as cutouts, photos or design. | ||
<noinclude></translate></noinclude><section end=req9 /></b> | <noinclude></translate></noinclude><section end=req9 /></b> | ||
| − | <b>10. <section begin=req10 /><noinclude><translate></noinclude>Demonstrate the ability to solve the following proportion problems: | + | <b>10. <section begin=req10 /><noinclude><translate><!--T:28--> |
| + | </noinclude>Demonstrate the ability to solve the following proportion problems: | ||
<noinclude></translate></noinclude><section end=req10 /></b> | <noinclude></translate></noinclude><section end=req10 /></b> | ||
| − | :<b>a. <section begin=req10a /><noinclude><translate></noinclude>At 60 km/h I travel between two cities in two hours. Traveling at 80 km/h, what is the estimated time to travel this route? | + | :<b>a. <section begin=req10a /><noinclude><translate><!--T:29--> |
| + | </noinclude>At 60 km/h I travel between two cities in two hours. Traveling at 80 km/h, what is the estimated time to travel this route? | ||
<noinclude></translate></noinclude><section end=req10a /></b> | <noinclude></translate></noinclude><section end=req10a /></b> | ||
| − | :<b>b. <section begin=req10b /><noinclude><translate></noinclude>At an average of 90 km/h, I can make a journey in three hours. To make this journey in just two hours, what should my average speed be? | + | :<b>b. <section begin=req10b /><noinclude><translate><!--T:30--> |
| + | </noinclude>At an average of 90 km/h, I can make a journey in three hours. To make this journey in just two hours, what should my average speed be? | ||
<noinclude></translate></noinclude><section end=req10b /></b> | <noinclude></translate></noinclude><section end=req10b /></b> | ||
| − | :<b>c. <section begin=req10c /><noinclude><translate></noinclude>If 20 men working for 20 days build 500 meters of a wall, how many men will it take to build 1000 meters more of this wall in 30 days? | + | :<b>c. <section begin=req10c /><noinclude><translate><!--T:31--> |
| + | </noinclude>If 20 men working for 20 days build 500 meters of a wall, how many men will it take to build 1000 meters more of this wall in 30 days? | ||
<noinclude></translate></noinclude><section end=req10c /></b> | <noinclude></translate></noinclude><section end=req10c /></b> | ||
| − | <b>11. <section begin=req11 /><noinclude><translate></noinclude>Demonstrate the ability to solve problem situations involving equations: | + | <b>11. <section begin=req11 /><noinclude><translate><!--T:32--> |
| + | </noinclude>Demonstrate the ability to solve problem situations involving equations: | ||
<noinclude></translate></noinclude><section end=req11 /></b> | <noinclude></translate></noinclude><section end=req11 /></b> | ||
| − | :<b>a. <section begin=req11a /><noinclude><translate></noinclude>I have the following choice: I buy 20 units of a product with all the money I have, or buy only 14 units of a project with all the money I have, or buy only 14 units and I still have $15.00 in change. What is the unit value of this product? | + | :<b>a. <section begin=req11a /><noinclude><translate><!--T:33--> |
| + | </noinclude>I have the following choice: I buy 20 units of a product with all the money I have, or buy only 14 units of a project with all the money I have, or buy only 14 units and I still have $15.00 in change. What is the unit value of this product? | ||
<noinclude></translate></noinclude><section end=req11a /></b> | <noinclude></translate></noinclude><section end=req11a /></b> | ||
| − | :<b>b. <section begin=req11b /><noinclude><translate></noinclude>What is the root of the equation 7x - 2 = -4x + 5? | + | :<b>b. <section begin=req11b /><noinclude><translate><!--T:34--> |
| + | </noinclude>What is the root of the equation 7x - 2 = -4x + 5? | ||
<noinclude></translate></noinclude><section end=req11b /></b> | <noinclude></translate></noinclude><section end=req11b /></b> | ||
| − | :<b>c. <section begin=req11c /><noinclude><translate></noinclude>If I add 8 to the amount of toy cars I own, I will have the same amount of cars as my brother if, of the 28 that he owns, the amount that I own is subtracted. How many toy cars do I have? | + | :<b>c. <section begin=req11c /><noinclude><translate><!--T:35--> |
| + | </noinclude>If I add 8 to the amount of toy cars I own, I will have the same amount of cars as my brother if, of the 28 that he owns, the amount that I own is subtracted. How many toy cars do I have? | ||
<noinclude></translate></noinclude><section end=req11c /></b> | <noinclude></translate></noinclude><section end=req11c /></b> | ||
<section end=Body /> | <section end=Body /> | ||
<noinclude><translate> | <noinclude><translate> | ||
| + | <!--T:36--> | ||
[[Category:Honor Requirements|{{#titleparts:{{PAGENAME}}|1|2}}]] | [[Category:Honor Requirements|{{#titleparts:{{PAGENAME}}|1|2}}]] | ||
[[Category:Honor Requirements Revision 3|{{#titleparts:{{PAGENAME}}|1|2}}]] | [[Category:Honor Requirements Revision 3|{{#titleparts:{{PAGENAME}}|1|2}}]] | ||
</translate></noinclude> | </translate></noinclude> | ||
Revision as of 15:25, 8 March 2021
Math Skills III
Authority:
Category:
Skill Level:
Year Introduced:
![]()
1. Have the Math Skills II honor.
2. Solve the following operations using the traditional algorithm:
- a. 641 + 135
- b. 845 - 124
- c. 34 x 125
- d. 856 ÷ 24
3. Identify and classify the numerical sets.
4. Demonstrate the ability to solve the following equations:
- a. 2x - 10 = -4x + 14
- b. 18x - 43 = 65
- c. 23x - 16 = 14 - 17x
- d. 10y - 5(1 + y) = 3(2y - 2) - 20
- e. x(x + 4) + x(x + 2) = 2x² + 12
- f. (x - 5) / 10 + (1 - 2x) / 5 = (3-x) / 4
- g. 4x(x + 6) - x² = 5x²
5. Demonstrate the ability to solve the following products:
- a. (x + 3y)²
- b. (a5 + 2bc)²
- c. (3x + y²)²
- d. (1 + 5m)(1 - 5m)
- e. (ab - c)²
- f. (m - 1)³
- g. (a³ - b³) (a³ + b³)
6. Calculate the area of the following figures:
7. In the Orienteering honor, the Pathfinder must have knowledge of angles to know how to use cartographic charts and to use a compass. Demonstrate the ability to convert angles to minutes, minutes to seconds, showing three practical examples.
8. In the Pioneering honor, we learned to build camp furniture, which has a whole mathematical relationship. Design and present some camp furniture where geometric shapes appear and classify each one. Cite three examples.
9. Present a poster showing ten practical examples of geometric figures used in a daily routine. It can be as cutouts, photos or design.
10. Demonstrate the ability to solve the following proportion problems:
- a. At 60 km/h I travel between two cities in two hours. Traveling at 80 km/h, what is the estimated time to travel this route?
- b. At an average of 90 km/h, I can make a journey in three hours. To make this journey in just two hours, what should my average speed be?
- c. If 20 men working for 20 days build 500 meters of a wall, how many men will it take to build 1000 meters more of this wall in 30 days?
11. Demonstrate the ability to solve problem situations involving equations:
- a. I have the following choice: I buy 20 units of a product with all the money I have, or buy only 14 units of a project with all the money I have, or buy only 14 units and I still have $15.00 in change. What is the unit value of this product?
- b. What is the root of the equation 7x - 2 = -4x + 5?
- c. If I add 8 to the amount of toy cars I own, I will have the same amount of cars as my brother if, of the 28 that he owns, the amount that I own is subtracted. How many toy cars do I have?
