Difference between revisions of "AY Honors/Math Skills III/es"
(Created page with "Especialidades JA/Habilidad matemática III") |
(Created page with "<nowiki/>{{honor_landing |honorname=Habilidad matemática III |skill=3 |year=2012 |category=Health and Science |authority=South American Division |insignia=Math Skills III Hon...") |
||
| Line 1: | Line 1: | ||
<nowiki/>{{honor_landing | <nowiki/>{{honor_landing | ||
| − | |honorname= | + | |honorname=Habilidad matemática III |
|skill=3 | |skill=3 | ||
|year=2012 | |year=2012 | ||
Revision as of 15:25, 8 March 2021
| Habilidad matemática III | |
|---|---|
| Salud y ciencia | |
Nivel de destreza 123 | |
Autoridad de aprobación División Sudamericana | Año de introducción 2012 |
Vea también | |
AY Honors/Math Skills III/Overview/es
El requisito más desafiante de esta especialidad es probablemente el siguiente:
5. Demostrar habilidad de resolver los siguientes productos notables:
- a. (x + 3y)²
- b. (a5 + 2bc)²
- c. (3x + y²)²
- d. (1 + 5m)(1 - 5m)
- e. (ab - c)²
- f. (m - 1)³
- g. (a³ - b³) (a³ + b³)
1. Tener la especialidad de Habilidad matemática II.
2. Resolver las siguientes operaciones usando el algoritmo tradicional:
- a. 641 + 135
- b. 845 - 124
- c. 34 x 125
- d. 856 ÷ 24
3. Identificar y clasificar los conjuntos numéricos.
4. Demostrar habilidad de resolver las siguientes ecuaciones:
- a. 2x - 10 = -4x + 14
- b. 18x - 43 = 65
- c. 23x - 16 = 14 - 17x
- d. 10y - 5(1 + y) = 3(2y - 2) - 20
- e. x(x + 4) + x(x + 2) = 2x² + 12
- f. (x - 5) / 10 + (1 - 2x) / 5 = (3-x) / 4
- g. 4x(x + 6) - x² = 5x²
5. Demostrar habilidad de resolver los siguientes productos notables:
- a. (x + 3y)²
- b. (a5 + 2bc)²
- c. (3x + y²)²
- d. (1 + 5m)(1 - 5m)
- e. (ab - c)²
- f. (m - 1)³
- g. (a³ - b³) (a³ + b³)
6. Calcular el área de las siguientes figuras:
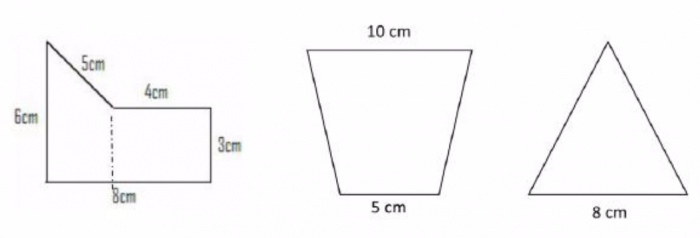
7. En la especialidad de Orientación, el Conquistador debe tener conocimientos de ángulo, para saber usar carta cartográfica y usar una brújula. Demostrar habilidad de convertir ángulos a minutos, minutos a segundos, mostrando tres ejemplos prácticos.
8. En la especialidad de Pionerismo aprendimos a construir muebles de campaña, que a su vez tienen toda una relación matemática. Diseñar y presentar algunos muebles de campaña donde aparezcan formas geométricas y clasificar cada uno. Citar tres ejemplos.
9. Presentar un afiche mostrando diez ejemplos prácticos de figuras geométricas usadas en la rutina diaria. Puede ser en forma de figuras recortadas, fotos o diseño.
10. Demostrar habilidad para resolver los siguientes problemas de proporción:
- a. A 60 km/h hago el trayecto entre dos ciudades en dos horas. Transitando a 80 km/h. ¿Cuál es el tiempo estimado para recorrer este trayecto?
- b. Al promedio de 90 km/h, hago un trayecto en tres horas. Para hacer este trayecto en sólo dos horas, ¿cuál debe ser mi velocidad promedio?
- c. Si 20 hombres trabajando durante 20 días construyen 500 metros de un muro, ¿cuántos hombres serán necesarios para construir 1000 metros más de este muro en 30 días?
11. Demostrar habilidad para resolver situaciones problemas involucrando ecuaciones:
- a. Tengo la siguiente elección: O compro 20 unidades de un producto con todo el dinero que tengo, o compro sólo 14 unidades de un proyecto con todo el dinero que tengo, o compro sólo 14 unidades y aún me sobra un cambio de $15. ¿Cuál es el valor unitario de este producto?
- b. ¿Cuál es la raíz de la ecuación 7x - 2 = -4x + 5?
- c. Si agrego 8 a la cantidad de carritos que poseo, me quedaré con la misma cantidad de carritos que mi hermano, si de los 28 que él posee, se le saca la cantidad que poseo. ¿Cuántos carritos tengo?
1
Para consejos e instrucciones, véase Habilidad matemática II.
2
2a
2b
2c
2d
3
4
4a
4b
4c
4d
4e
4f
4g
5
5a
5b
5c
5d
5e
5f
5g
7
8
9
10
10a
10b
10c
11
11a
11b
11c
Referencias
- Pages using DynamicPageList3 parser function
- Categoría: Tiene imagen de insignia
- AY Honors/Honor landing/es
- Categoría:Especialidades JA/Salud y ciencia
- AY Honors/Introduced in 2012/es
- Categoría:Especialidades JA/Nivel de destreza 3
- Categoría:Especialidades JA/Aprobadas por la División Sudamericana
- AY Honors/See Also/Math Skills IV/es
- AY Honors/See Also/Math Skills II/es


