Difference between revisions of "AY Honors/Math Skills III/Requirements/es"
(Created page with "</noinclude>Al promedio de 90 km/h, hago un trayecto en tres horas. Para hacer este trayecto en sólo dos horas, ¿cuál debe ser mi velocidad promedio? <noinclude>") |
(Created page with "</noinclude>Si 20 hombres trabajando durante 20 días construyen 500 metros de un muro, ¿cuántos hombres serán necesarios para construir 1000 metros más de este muro en 30...") |
||
| Line 95: | Line 95: | ||
<noinclude></noinclude><section end=req10b /></b> | <noinclude></noinclude><section end=req10b /></b> | ||
| − | :<b>c. <section begin=req10c /><noinclude></noinclude> | + | :<b>c. <section begin=req10c /><noinclude></noinclude>Si 20 hombres trabajando durante 20 días construyen 500 metros de un muro, ¿cuántos hombres serán necesarios para construir 1000 metros más de este muro en 30 días? |
<noinclude></noinclude><section end=req10c /></b> | <noinclude></noinclude><section end=req10c /></b> | ||
Revision as of 15:32, 8 March 2021
Habilidad matemática III
Autoridad:
Categoría:
Destreza:
Año de introducción:
![]()
1. Tener la especialidad de Habilidad matemática II
2. Resolver las siguientes operaciones usando el algoritmo tradicional:
- a. 641 + 135
- b. 845 - 124
- c. 34 x 125
- d. 856 ÷ 24
3. Identificar y clasificar los conjuntos numéricos.
4. Demostrar habilidad de resolver las siguientes ecuaciones:
- a. 2x - 10 = -4x + 14
- b. 18x - 43 = 65
- c. 23x - 16 = 14 - 17x
- d. 10y - 5(1 + y) = 3(2y - 2) - 20
- e. x(x + 4) + x(x + 2) = 2x² + 12
- f. (x - 5) / 10 + (1 - 2x) / 5 = (3-x) / 4
- g. 4x(x + 6) - x² = 5x²
5. Demostrar habilidad de resolver los siguientes productos notables:
- a. (x + 3y)²
- b. (a5 + 2bc)²
- c. (3x + y²)²
- d. (1 + 5m)(1 - 5m)
- e. (ab - c)²
- f. (m - 1)³
- g. (a³ - b³) (a³ + b³)
6. Calcular el área de las siguientes figuras:
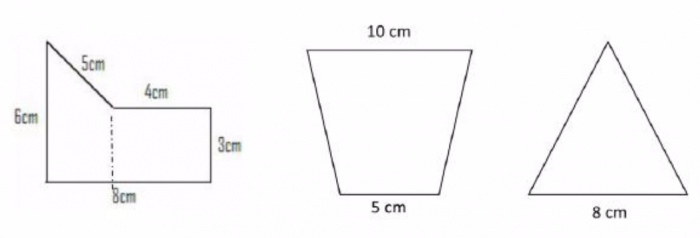
7. En la especialidad de Orientación, el Conquistador debe tener conocimientos de ángulo, para saber usar carta cartográfica y usar una brújula. Demostrar habilidad de convertir ángulos a minutos, minutos a segundos, mostrando tres ejemplos prácticos.
8. En la especialidad de Pionerismo aprendimos a construir muebles de campaña, que a su vez tienen toda una relación matemática. Diseñar y presentar algunos muebles de campaña donde aparezcan formas geométricas y clasificar cada uno. Citar tres ejemplos.
9. Presentar un afiche mostrando diez ejemplos prácticos de figuras geométricas usadas en la rutina diaria. Puede ser en forma de figuras recortadas, fotos o diseño.
10. Demuestra habilidad para resolver los siguientes problemas de proporción:
- a. A 60 km/h hago el trayecto entre dos ciudades en dos horas. Transitando a 80 km/h. ¿Cuál es el tiempo estimado para recorrer este trayecto?
- b. Al promedio de 90 km/h, hago un trayecto en tres horas. Para hacer este trayecto en sólo dos horas, ¿cuál debe ser mi velocidad promedio?
- c. Si 20 hombres trabajando durante 20 días construyen 500 metros de un muro, ¿cuántos hombres serán necesarios para construir 1000 metros más de este muro en 30 días?
11. Demonstrate the ability to solve problem situations involving equations:
- a. I have the following choice: I buy 20 units of a product with all the money I have, or buy only 14 units of a project with all the money I have, or buy only 14 units and I still have $15.00 in change. What is the unit value of this product?
- b. What is the root of the equation 7x - 2 = -4x + 5?
- c. If I add 8 to the amount of toy cars I own, I will have the same amount of cars as my brother if, of the 28 that he owns, the amount that I own is subtracted. How many toy cars do I have?
