Difference between revisions of "AY Honors/Math Skills III/Requirements/pt-br"
(Created page with "</noinclude>18x - 43 = 65 <noinclude>") |
(Created page with "</noinclude>(x + 3y)² <noinclude>") |
||
| Line 39: | Line 39: | ||
<noinclude></noinclude><section end=req4d /></b> | <noinclude></noinclude><section end=req4d /></b> | ||
| − | :<b>e. <section begin=req4e /><noinclude> | + | :<b>e. <section begin=req4e /><noinclude></noinclude>x(x + 4) + x(x + 2) = 2x² + 12 |
| − | </noinclude>x(x + 4) + x(x + 2) = 2x² + 12 | + | <noinclude></noinclude><section end=req4e /></b> |
| − | <noinclude | ||
| − | |||
| − | :<b>f. <section begin=req4f /><noinclude> | + | :<b>f. <section begin=req4f /><noinclude></noinclude>(x - 5) / 10 + (1 - 2x) / 5 = (3-x) / 4 |
| − | </noinclude>(x - 5) / 10 + (1 - 2x) / 5 = (3-x) / 4 | + | <noinclude></noinclude><section end=req4f /></b> |
| − | <noinclude | ||
| − | |||
| − | :<b>g. <section begin=req4g /><noinclude> | + | :<b>g. <section begin=req4g /><noinclude></noinclude>4x(x + 6) - x² = 5x² |
| − | </noinclude>4x(x + 6) - x² = 5x² | + | <noinclude></noinclude><section end=req4g /></b> |
| − | <noinclude | ||
| − | |||
<section begin=challenge /> | <section begin=challenge /> | ||
| − | <b>5. <section begin=req5 /><noinclude> | + | <b>5. <section begin=req5 /><noinclude></noinclude>Demonstrar habilidade de resolver os seguintes produtos notáveis: |
| − | </noinclude> | + | <noinclude></noinclude><section end=req5 /></b> |
| − | <noinclude | ||
| − | |||
| − | :<b>a. <section begin=req5a /><noinclude> | + | :<b>a. <section begin=req5a /><noinclude></noinclude>(x + 3y)² |
| − | </noinclude>(x + 3y)² | + | <noinclude></noinclude><section end=req5a /></b> |
| − | <noinclude | ||
| − | |||
| − | :<b>b. <section begin=req5b /><noinclude> | + | :<b>b. <section begin=req5b /><noinclude></noinclude>(a<sup>5</sup> + 2bc)² |
| − | </noinclude>(a<sup>5</sup> + 2bc)² | + | <noinclude></noinclude><section end=req5b /></b> |
| − | <noinclude | ||
| − | |||
| − | :<b>c. <section begin=req5c /><noinclude> | + | :<b>c. <section begin=req5c /><noinclude></noinclude>(3x + y²)² |
| − | </noinclude>(3x + y²)² | + | <noinclude></noinclude><section end=req5c /></b> |
| − | <noinclude | ||
| − | |||
| − | :<b>d. <section begin=req5d /><noinclude> | + | :<b>d. <section begin=req5d /><noinclude></noinclude>(1 + 5m)(1 - 5m) |
| − | </noinclude>(1 + 5m)(1 - 5m) | + | <noinclude></noinclude><section end=req5d /></b> |
| − | <noinclude | ||
| − | |||
| − | :<b>e. <section begin=req5e /><noinclude> | + | :<b>e. <section begin=req5e /><noinclude></noinclude>(ab - c)² |
| − | </noinclude>(ab - c)² | + | <noinclude></noinclude><section end=req5e /></b> |
| − | <noinclude | ||
| − | |||
| − | :<b>f. <section begin=req5f /><noinclude> | + | :<b>f. <section begin=req5f /><noinclude></noinclude>(m - 1)³ |
| − | </noinclude>(m - 1)³ | + | <noinclude></noinclude><section end=req5f /></b> |
| − | <noinclude | ||
| − | |||
| − | :<b>g. <section begin=req5g /><noinclude> | + | :<b>g. <section begin=req5g /><noinclude></noinclude>(a³ - b³) (a³ + b³) |
| − | </noinclude>(a³ - b³) (a³ + b³) | + | <noinclude></noinclude><section end=req5g /></b> |
| − | <noinclude | ||
| − | |||
<section end=challenge /> | <section end=challenge /> | ||
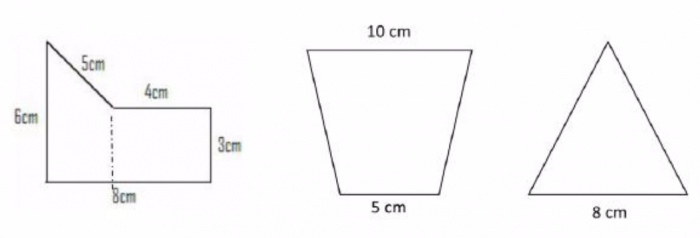
| − | <b>6. <section begin=req6 /><noinclude> | + | <b>6. <section begin=req6 /><noinclude></noinclude>Calcular a área das seguintes figuras planas: |
| − | </noinclude> | ||
[[File:Math Skills III figures.png|700px]] | [[File:Math Skills III figures.png|700px]] | ||
| − | <noinclude | + | <noinclude></noinclude><section end=req6 /></b> |
| − | |||
<b>7. <section begin=req7 /><noinclude><div lang="en" dir="ltr" class="mw-content-ltr"> | <b>7. <section begin=req7 /><noinclude><div lang="en" dir="ltr" class="mw-content-ltr"> | ||
Revision as of 16:54, 10 June 2021
Nível de Habilidade
3
Ano
2012
Version
11.02.2026
Autoridade de Aprovação
Divisão Sul Americana
1. Ter a especialidade Habilidades em matemática II.
2. Resolver as seguintes operações usando o algoritmo tradicional:
- a. 641 + 135
- b. 845 - 124
- c. 34 x 125
- d. 856 ÷ 24
3. Identificar e classificar os conjuntos numéricos.
4. Demonstrar habilidade de resolver as seguintes equações:
- a. 2x - 10 = -4x + 14
- b. 18x - 43 = 65
- c. 23x - 16 = 14 - 17x
- d. 10y - 5(1 + y) = 3(2y - 2) - 20
- e. x(x + 4) + x(x + 2) = 2x² + 12
- f. (x - 5) / 10 + (1 - 2x) / 5 = (3-x) / 4
- g. 4x(x + 6) - x² = 5x²
5. Demonstrar habilidade de resolver os seguintes produtos notáveis:
- a. (x + 3y)²
- b. (a5 + 2bc)²
- c. (3x + y²)²
- d. (1 + 5m)(1 - 5m)
- e. (ab - c)²
- f. (m - 1)³
- g. (a³ - b³) (a³ + b³)
6. Calcular a área das seguintes figuras planas:
In the Orienteering honor, the Pathfinder must have knowledge of angles to know how to use cartographic charts and to use a compass. Demonstrate the ability to convert angles to minutes, minutes to seconds, showing three practical examples.
In the Pioneering honor, we learned to build camp furniture, which has a whole mathematical relationship. Design and present some camp furniture where geometric shapes appear and classify each one. Cite three examples.
Present a poster showing ten practical examples of geometric figures used in a daily routine. It can be as cutouts, photos or design.
Demonstrate the ability to solve the following proportion problems:
- a.
At 60 km/h I travel between two cities in two hours. Traveling at 80 km/h, what is the estimated time to travel this route?
- b.
At an average of 90 km/h, I can make a journey in three hours. To make this journey in just two hours, what should my average speed be?
- c.
If 20 men working for 20 days build 500 meters of a wall, how many men will it take to build 1000 meters more of this wall in 30 days?
Demonstrate the ability to solve problem situations involving equations:
- a.
I have the following choice: I buy 20 units of a product with all the money I have, or buy only 14 units of a project with all the money I have, or buy only 14 units and I still have $15.00 in change. What is the unit value of this product?
- b.
What is the root of the equation 7x - 2 = -4x + 5?
- c.
If I add 8 to the amount of toy cars I own, I will have the same amount of cars as my brother if, of the 28 that he owns, the amount that I own is subtracted. How many toy cars do I have?



