Difference between revisions of "AY Honors/Math Skills III/Requirements/pt-br"

From Pathfinder Wiki
< AY Honors‎ | Math Skills IIIAY Honors/Math Skills III/Requirements/pt-br
(Created page with "</noinclude>Ter a especialidade Habilidades em matemática II. <noinclude>")
(Updating to match new version of source page)
 
(6 intermediate revisions by 2 users not shown)
Line 36: Line 36:
 
<noinclude></noinclude><section end=req4c /></b>
 
<noinclude></noinclude><section end=req4c /></b>
  
−
:<b>d. <section begin=req4d /><noinclude><div lang="en" dir="ltr" class="mw-content-ltr">
+
:<b>d. <section begin=req4d /><noinclude></noinclude>10y - 5(1 + y) = 3(2y - 2) - 20
−
</noinclude>10y - 5(1 + y) = 3(2y - 2) - 20
+
<noinclude></noinclude><section end=req4d /></b>
−
<noinclude>
 
−
</div></noinclude><section end=req4d /></b>
 
  
−
:<b>e. <section begin=req4e /><noinclude><div lang="en" dir="ltr" class="mw-content-ltr">
+
:<b>e. <section begin=req4e /><noinclude></noinclude>x(x + 4) + x(x + 2) = 2x² + 12
−
</noinclude>x(x + 4) + x(x + 2) = 2x² + 12
+
<noinclude></noinclude><section end=req4e /></b>
−
<noinclude>
 
−
</div></noinclude><section end=req4e /></b>
 
  
−
:<b>f. <section begin=req4f /><noinclude><div lang="en" dir="ltr" class="mw-content-ltr">
+
:<b>f. <section begin=req4f /><noinclude></noinclude>(x - 5) / 10 + (1 - 2x) / 5 = (3-x) / 4
−
</noinclude>(x - 5) / 10 + (1 - 2x) / 5 = (3-x) / 4
+
<noinclude></noinclude><section end=req4f /></b>
−
<noinclude>
 
−
</div></noinclude><section end=req4f /></b>
 
  
−
:<b>g. <section begin=req4g /><noinclude><div lang="en" dir="ltr" class="mw-content-ltr">
+
:<b>g. <section begin=req4g /><noinclude></noinclude>4x(x + 6) - x² = 5x²
−
</noinclude>4x(x + 6) - x² = 5x²
+
<noinclude></noinclude><section end=req4g /></b>
−
<noinclude>
 
−
</div></noinclude><section end=req4g /></b>
 
  
 
<section begin=challenge />
 
<section begin=challenge />
−
<b>5. <section begin=req5 /><noinclude><div lang="en" dir="ltr" class="mw-content-ltr">
+
<b>5. <section begin=req5 /><noinclude></noinclude>Demonstrar habilidade de resolver os seguintes produtos notáveis:
−
</noinclude>Demonstrate the ability to solve the following products:
+
<noinclude></noinclude><section end=req5 /></b>
−
<noinclude>
 
−
</div></noinclude><section end=req5 /></b>
 
  
−
:<b>a. <section begin=req5a /><noinclude><div lang="en" dir="ltr" class="mw-content-ltr">
+
:<b>a. <section begin=req5a /><noinclude></noinclude>(x + 3y)²
−
</noinclude>(x + 3y)²
+
<noinclude></noinclude><section end=req5a /></b>
−
<noinclude>
 
−
</div></noinclude><section end=req5a /></b>
 
  
−
:<b>b. <section begin=req5b /><noinclude><div lang="en" dir="ltr" class="mw-content-ltr">
+
:<b>b. <section begin=req5b /><noinclude></noinclude>(a<sup>5</sup> + 2bc)²
−
</noinclude>(a<sup>5</sup> + 2bc)²
+
<noinclude></noinclude><section end=req5b /></b>
−
<noinclude>
 
−
</div></noinclude><section end=req5b /></b>
 
  
−
:<b>c. <section begin=req5c /><noinclude><div lang="en" dir="ltr" class="mw-content-ltr">
+
:<b>c. <section begin=req5c /><noinclude></noinclude>(3x + y²)²
−
</noinclude>(3x + y²)²
+
<noinclude></noinclude><section end=req5c /></b>
−
<noinclude>
 
−
</div></noinclude><section end=req5c /></b>
 
  
−
:<b>d. <section begin=req5d /><noinclude><div lang="en" dir="ltr" class="mw-content-ltr">
+
:<b>d. <section begin=req5d /><noinclude></noinclude>(1 + 5m)(1 - 5m)
−
</noinclude>(1 + 5m)(1 - 5m)
+
<noinclude></noinclude><section end=req5d /></b>
−
<noinclude>
 
−
</div></noinclude><section end=req5d /></b>
 
  
−
:<b>e. <section begin=req5e /><noinclude><div lang="en" dir="ltr" class="mw-content-ltr">
+
:<b>e. <section begin=req5e /><noinclude></noinclude>(ab - c)²
−
</noinclude>(ab - c)²
+
<noinclude></noinclude><section end=req5e /></b>
−
<noinclude>
 
−
</div></noinclude><section end=req5e /></b>
 
  
−
:<b>f. <section begin=req5f /><noinclude><div lang="en" dir="ltr" class="mw-content-ltr">
+
:<b>f. <section begin=req5f /><noinclude></noinclude>(m - 1)³
−
</noinclude>(m - 1)³
+
<noinclude></noinclude><section end=req5f /></b>
−
<noinclude>
 
−
</div></noinclude><section end=req5f /></b>
 
  
−
:<b>g. <section begin=req5g /><noinclude><div lang="en" dir="ltr" class="mw-content-ltr">
+
:<b>g. <section begin=req5g /><noinclude></noinclude>(a³ - b³) (a³ + b³)
−
</noinclude>(a³ - b³) (a³ + b³)
+
<noinclude></noinclude><section end=req5g /></b>
−
<noinclude>
 
−
</div></noinclude><section end=req5g /></b>
 
 
<section end=challenge />
 
<section end=challenge />
  
−
<b>6. <section begin=req6 /><noinclude><div lang="en" dir="ltr" class="mw-content-ltr">
+
<b>6. <section begin=req6 /><noinclude></noinclude>Calcular a área das seguintes figuras planas:
−
</noinclude>Calculate the area of ​​the following figures:
 
 
[[File:Math Skills III figures.png|700px]]
 
[[File:Math Skills III figures.png|700px]]
−
<noinclude>
+
<noinclude></noinclude><section end=req6 /></b>
−
</div></noinclude><section end=req6 /></b>
 
  
−
<b>7. <section begin=req7 /><noinclude><div lang="en" dir="ltr" class="mw-content-ltr">
+
<b>7. <section begin=req7 /><noinclude></noinclude>Na especialidade de [[AY Honors/Orienteering/pt-br|Orientação]], o desbravador precisa ter conhecimentos de ângulo, para saber usar carta cartográfica e usar uma bússola. Demonstrar habilidade de converter ângulos para minutos, minutos para segundos, mostrando três exemplos práticos.
−
</noinclude>In the [[Adventist_Youth_Honors_Answer_Book/Recreation/Orienteering|Orienteering]] honor, the Pathfinder must have knowledge of angles to know how to use cartographic charts and to use a compass. Demonstrate the ability to convert angles to minutes, minutes to seconds, showing three practical examples.
+
<noinclude></noinclude><section end=req7 /></b>
−
<noinclude>
 
−
</div></noinclude><section end=req7 /></b>
 
  
−
<b>8. <section begin=req8 /><noinclude><div lang="en" dir="ltr" class="mw-content-ltr">
+
<b>8. <section begin=req8 /><noinclude></noinclude>Na especialidade de [[AY Honors/Pioneering/pt-br|Pioneiria]], aprendemos a construir móveis de campanha, que por sua vez tem toda uma relação matemática. Desenhar e apresentar alguns móveis de campanha onde aparecem formas geométricas e classificar cada um. Citar três exemplos.
−
</noinclude>In the [[Adventist_Youth_Honors_Answer_Book/Recreation/Pioneering|Pioneering]] honor, we learned to build camp furniture, which has a whole mathematical relationship. Design and present some camp furniture where geometric shapes appear and classify each one. Cite three examples.
+
<noinclude></noinclude><section end=req8 /></b>
−
<noinclude>
 
−
</div></noinclude><section end=req8 /></b>
 
  
−
<b>9. <section begin=req9 /><noinclude><div lang="en" dir="ltr" class="mw-content-ltr">
+
<b>9. <section begin=req9 /><noinclude></noinclude>Apresentar um cartaz mostrando dez exemplos práticos de figuras geométricas usadas no dia a dia. Pode ser em forma de figuras recortadas, fotos ou desenho.
−
</noinclude>Present a poster showing ten practical examples of geometric figures used in a daily routine. It can be as cutouts, photos or design.
+
<noinclude></noinclude><section end=req9 /></b>
−
<noinclude>
 
−
</div></noinclude><section end=req9 /></b>
 
  
−
<b>10. <section begin=req10 /><noinclude><div lang="en" dir="ltr" class="mw-content-ltr">
+
<b>10. <section begin=req10 /><noinclude></noinclude>Demonstre habilidade para resolver a solução dos seguintes problemas de proporção:
−
</noinclude>Demonstrate the ability to solve the following proportion problems:
+
<noinclude></noinclude><section end=req10 /></b>
−
<noinclude>
 
−
</div></noinclude><section end=req10 /></b>
 
  
−
:<b>a. <section begin=req10a /><noinclude><div lang="en" dir="ltr" class="mw-content-ltr">
+
:<b>a. <section begin=req10a /><noinclude></noinclude>A 60 km/h faço o percurso entre duas cidades em duas horas. Trafegando a 80 km qual o tempo estimado para percorrer este trajeto?
−
</noinclude>At 60 km/h I travel between two cities in two hours. Traveling at 80 km/h, what is the estimated time to travel this route?
+
<noinclude></noinclude><section end=req10a /></b>
−
<noinclude>
 
−
</div></noinclude><section end=req10a /></b>
 
  
−
:<b>b. <section begin=req10b /><noinclude><div lang="en" dir="ltr" class="mw-content-ltr">
+
:<b>b. <section begin=req10b /><noinclude></noinclude>À média de 90 km/h faço um trajeto em três horas. Para que eu faça este percurso em apenas duas horas, qual deve ser a minha velocidade média?
−
</noinclude>At an average of 90 km/h, I can make a journey in three hours. To make this journey in just two hours, what should my average speed be?
+
<noinclude></noinclude><section end=req10b /></b>
−
<noinclude>
 
−
</div></noinclude><section end=req10b /></b>
 
  
−
:<b>c. <section begin=req10c /><noinclude><div lang="en" dir="ltr" class="mw-content-ltr">
+
:<b>c. <section begin=req10c /><noinclude></noinclude>Se 20 homens trabalhando durante 15 dias constroem 500 metros de um muro, quantos homens serão necessários para construir mais 1000 metros deste muro em 30 dias?
−
</noinclude>If 20 men working for 20 days build 500 meters of a wall, how many men will it take to build 1000 meters more of this wall in 30 days?
+
<noinclude></noinclude><section end=req10c /></b>
−
<noinclude>
 
−
</div></noinclude><section end=req10c /></b>
 
  
−
<b>11. <section begin=req11 /><noinclude><div lang="en" dir="ltr" class="mw-content-ltr">
+
<b>11. <section begin=req11 /><noinclude></noinclude>Demonstre habilidade para resolver situações problemas envolvendo equações:
−
</noinclude>Demonstrate the ability to solve problem situations involving equations:
+
<noinclude></noinclude><section end=req11 /></b>
−
<noinclude>
 
−
</div></noinclude><section end=req11 /></b>
 
  
−
:<b>a. <section begin=req11a /><noinclude><div lang="en" dir="ltr" class="mw-content-ltr">
+
:<b>a. <section begin=req11a /><noinclude></noinclude>Tenho a seguinte escolha: Ou compro 20 unidades de um produto com todo o dinheiro que tenho, ou compro apenas 14 unidades e ainda me sobra um troco de R$ 30,00. Qual o valor unitário deste produto?
−
</noinclude>I have the following choice: I buy 20 units of a product with all the money I have, or buy only 14 units of a project with all the money I have, or buy only 14 units and I still have $15.00 in change. What is the unit value of this product?
+
<noinclude></noinclude><section end=req11a /></b>
−
<noinclude>
 
−
</div></noinclude><section end=req11a /></b>
 
  
−
:<b>b. <section begin=req11b /><noinclude><div lang="en" dir="ltr" class="mw-content-ltr">
+
:<b>b. <section begin=req11b /><noinclude></noinclude>Qual é a raiz da equação 7x - 2 = -4x + 5?
−
</noinclude>What is the root of the equation 7x - 2 = -4x + 5?  
+
<noinclude></noinclude><section end=req11b /></b>
−
<noinclude>
 
−
</div></noinclude><section end=req11b /></b>
 
  
−
:<b>c. <section begin=req11c /><noinclude><div lang="en" dir="ltr" class="mw-content-ltr">
+
:<b>c. <section begin=req11c /><noinclude></noinclude>Se eu adicionar 8 à quantidade de carrinhos que possuo, ficarei com a mesma quantidade de carrinhos de meu irmão, se dos 28 que ele possui, for retirada a quantidade que eu possuo. Quantos carrinhos eu tenho?
−
</noinclude>If I add 8 to the amount of toy cars I own, I will have the same amount of cars as my brother if, of the 28 that he owns, the amount that I own is subtracted. How many toy cars do I have?
+
<noinclude></noinclude><section end=req11c /></b>
−
<noinclude>
 
−
</div></noinclude><section end=req11c /></b>
 
 
<section end=Body />
 
<section end=Body />
−
 
−
<noinclude><div lang="en" dir="ltr" class="mw-content-ltr">
 
−
[[Category:Honor Requirements|{{#titleparts:{{PAGENAME}}|1|2}}]]
 
−
[[Category:Honor Requirements Revision 3|{{#titleparts:{{PAGENAME}}|1|2}}]]
 
−
<noinclude>
 
−
</div></noinclude>
 

Latest revision as of 03:33, 22 July 2022

Other languages:
English • ‎español • ‎français • ‎português do Brasil
Habilidades em matemática III

Nível de Habilidade

3

Ano

2012

Version

22.11.2024

Autoridade de Aprovação

Divisão Sul Americana

Math Skills III AY Honor.png
Habilidades em matemática III
Ciência e Saúde
Nível de Habilidade
123
Autoridade de Aprovação
Divisão Sul Americana
Ano de Introdução
2012
Veja também
Habilidades em matemática II
Habilidades em matemática IV
Habilidades em matemática IV



1. Ter a especialidade Habilidades em matemática II.

2. Resolver as seguintes operações usando o algoritmo tradicional:

a. 641 + 135

b. 845 - 124

c. 34 x 125

d. 856 ÷ 24

3. Identificar e classificar os conjuntos numéricos.

4. Demonstrar habilidade de resolver as seguintes equações:

a. 2x - 10 = -4x + 14

b. 18x - 43 = 65

c. 23x - 16 = 14 - 17x

d. 10y - 5(1 + y) = 3(2y - 2) - 20

e. x(x + 4) + x(x + 2) = 2x² + 12

f. (x - 5) / 10 + (1 - 2x) / 5 = (3-x) / 4

g. 4x(x + 6) - x² = 5x²


5. Demonstrar habilidade de resolver os seguintes produtos notáveis:

a. (x + 3y)²

b. (a5 + 2bc)²

c. (3x + y²)²

d. (1 + 5m)(1 - 5m)

e. (ab - c)²

f. (m - 1)³

g. (a³ - b³) (a³ + b³)


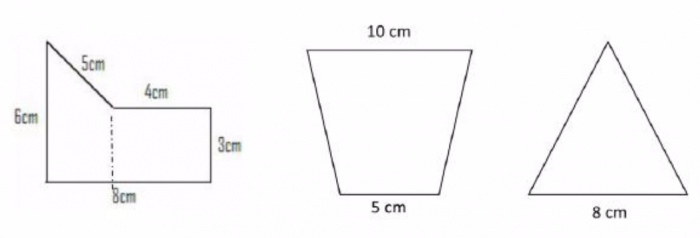
6. Calcular a área das seguintes figuras planas: Math Skills III figures.png

7. Na especialidade de Orientação, o desbravador precisa ter conhecimentos de ângulo, para saber usar carta cartográfica e usar uma bússola. Demonstrar habilidade de converter ângulos para minutos, minutos para segundos, mostrando três exemplos práticos.

8. Na especialidade de Pioneiria, aprendemos a construir móveis de campanha, que por sua vez tem toda uma relação matemática. Desenhar e apresentar alguns móveis de campanha onde aparecem formas geométricas e classificar cada um. Citar três exemplos.

9. Apresentar um cartaz mostrando dez exemplos práticos de figuras geométricas usadas no dia a dia. Pode ser em forma de figuras recortadas, fotos ou desenho.

10. Demonstre habilidade para resolver a solução dos seguintes problemas de proporção:

a. A 60 km/h faço o percurso entre duas cidades em duas horas. Trafegando a 80 km qual o tempo estimado para percorrer este trajeto?

b. À média de 90 km/h faço um trajeto em três horas. Para que eu faça este percurso em apenas duas horas, qual deve ser a minha velocidade média?

c. Se 20 homens trabalhando durante 15 dias constroem 500 metros de um muro, quantos homens serão necessários para construir mais 1000 metros deste muro em 30 dias?

11. Demonstre habilidade para resolver situações problemas envolvendo equações:

a. Tenho a seguinte escolha: Ou compro 20 unidades de um produto com todo o dinheiro que tenho, ou compro apenas 14 unidades e ainda me sobra um troco de R$ 30,00. Qual o valor unitário deste produto?

b. Qual é a raiz da equação 7x - 2 = -4x + 5?

c. Se eu adicionar 8 à quantidade de carrinhos que possuo, ficarei com a mesma quantidade de carrinhos de meu irmão, se dos 28 que ele possui, for retirada a quantidade que eu possuo. Quantos carrinhos eu tenho?

Retrieved from "https://wiki.pathfindersonline.org/index.php?title=AY_Honors/Math_Skills_III/Requirements/pt-br&oldid=577137"