Difference between revisions of "AY Honors/Math Skills III/Answer Key"
From Pathfinder Wiki
< AY Honors | Math Skills IIIAY Honors/Math Skills III/Answer Key
(+ Math Skills III SAD honor requirements) |
(Marked this version for translation) |
||
| Line 1: | Line 1: | ||
<languages /><br /> | <languages /><br /> | ||
| − | <noinclude><translate></noinclude> | + | <noinclude><translate><!--T:1--> |
| + | </noinclude> | ||
{{honor_desc | {{honor_desc | ||
|stage=00 | |stage=00 | ||
| Line 12: | Line 13: | ||
}} | }} | ||
| − | ==1. Have the Math Skills II honor.== | + | ==1. Have the Math Skills II honor.== <!--T:2--> |
{{honor_prerequisite|category=Health and Science|honor=Math Skills II}} | {{honor_prerequisite|category=Health and Science|honor=Math Skills II}} | ||
| − | ==2. Solve the following operations using the traditional algorithm:== | + | ==2. Solve the following operations using the traditional algorithm:== <!--T:3--> |
| − | ===a. 641 + 135=== | + | ===a. 641 + 135=== <!--T:4--> |
| − | ===b. 845 - 124=== | + | ===b. 845 - 124=== <!--T:5--> |
| − | ===c. 34 x 125=== | + | ===c. 34 x 125=== <!--T:6--> |
| − | ===d. 856 ÷ 24=== | + | ===d. 856 ÷ 24=== <!--T:7--> |
| − | ==3. Identify and classify the numerical sets.== | + | ==3. Identify and classify the numerical sets.== <!--T:8--> |
| − | ==4. Demonstrate the ability to solve the following equations:== | + | ==4. Demonstrate the ability to solve the following equations:== <!--T:9--> |
| − | ===a. 2x - 10 = -4x + 14=== | + | ===a. 2x - 10 = -4x + 14=== <!--T:10--> |
| − | ===b. 18x - 43 = 65=== | + | ===b. 18x - 43 = 65=== <!--T:11--> |
| − | ===c. 23x - 16 = 14 - 17x=== | + | ===c. 23x - 16 = 14 - 17x=== <!--T:12--> |
| − | ===d. 10y - 5(1 + y) = 3(2y - 2) - 20=== | + | ===d. 10y - 5(1 + y) = 3(2y - 2) - 20=== <!--T:13--> |
| − | ===e. x(x + 4) + x(x + 2) = 2x² + 12=== | + | ===e. x(x + 4) + x(x + 2) = 2x² + 12=== <!--T:14--> |
| − | ===f. (x = 5) / 10 + (1 - 2x) / 5 = (3-x) / 4=== | + | ===f. (x = 5) / 10 + (1 - 2x) / 5 = (3-x) / 4=== <!--T:15--> |
| − | ===g. 4x(x + 6) - x² = 5x²=== | + | ===g. 4x(x + 6) - x² = 5x²=== <!--T:16--> |
| − | ==5. Demonstrate the ability to solve the following products:== | + | ==5. Demonstrate the ability to solve the following products:== <!--T:17--> |
| − | ===a. (x + 3y)=== | + | ===a. (x + 3y)=== <!--T:18--> |
| − | ===b. (a5 + 2bc)²=== | + | ===b. (a5 + 2bc)²=== <!--T:19--> |
| − | ===c. (3x + y²)²=== | + | ===c. (3x + y²)²=== <!--T:20--> |
| − | ===d. (1 + 5m)(1 - 5m)=== | + | ===d. (1 + 5m)(1 - 5m)=== <!--T:21--> |
| − | ===e. (ab - c)²=== | + | ===e. (ab - c)²=== <!--T:22--> |
| − | ===f. (m - 1)³=== | + | ===f. (m - 1)³=== <!--T:23--> |
| − | ===g. (a³ - b³) (a³ + b³)=== | + | ===g. (a³ - b³) (a³ + b³)=== <!--T:24--> |
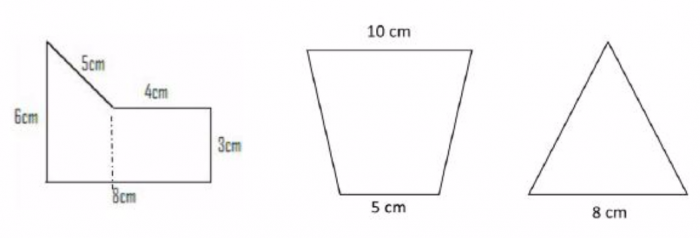
| − | ==6. Calculate the area of the following figures:== | + | ==6. Calculate the area of the following figures:== <!--T:25--> |
| + | <!--T:26--> | ||
[[File:Math Skills III figures.png|700px]] | [[File:Math Skills III figures.png|700px]] | ||
| − | ==7. In the [[Adventist_Youth_Honors_Answer_Book/Recreation/Orienteering|Orienteering]] honor, the Pathfinder must have knowledge of angles to know how to use cartographic charts and to use a compass. Demonstrate the ability to convert angles to minutes, minutes to seconds, showing three practical examples.== | + | ==7. In the [[Adventist_Youth_Honors_Answer_Book/Recreation/Orienteering|Orienteering]] honor, the Pathfinder must have knowledge of angles to know how to use cartographic charts and to use a compass. Demonstrate the ability to convert angles to minutes, minutes to seconds, showing three practical examples.== <!--T:27--> |
| − | ==8. In the [[Adventist_Youth_Honors_Answer_Book/Recreation/Pioneering|Pioneering]] honor, we learned to build camp furniture, which has a whole mathematical relationship. Design and present some camp furniture where geometric shapes appear and classify each one. Cite three examples.== | + | ==8. In the [[Adventist_Youth_Honors_Answer_Book/Recreation/Pioneering|Pioneering]] honor, we learned to build camp furniture, which has a whole mathematical relationship. Design and present some camp furniture where geometric shapes appear and classify each one. Cite three examples.== <!--T:28--> |
| − | ==9. Present a poster showing ten practical examples of geometric figures used in a daily routine. It can be as cutouts, photos or design.== | + | ==9. Present a poster showing ten practical examples of geometric figures used in a daily routine. It can be as cutouts, photos or design.== <!--T:29--> |
| − | ==10. Demonstrate the ability to solve the following proportion problems:== | + | ==10. Demonstrate the ability to solve the following proportion problems:== <!--T:30--> |
| − | ===a. At 60 km/h I travel between two cities in two hours. Traveling at 80 km/h, what is the estimated time to travel this route?=== | + | ===a. At 60 km/h I travel between two cities in two hours. Traveling at 80 km/h, what is the estimated time to travel this route?=== <!--T:31--> |
| − | ===b. At an average of 90 km/h, I can make a journey in three hours. To make this journey in just two hours, what should my average speed be?=== | + | ===b. At an average of 90 km/h, I can make a journey in three hours. To make this journey in just two hours, what should my average speed be?=== <!--T:32--> |
| − | ===c. If 20 men working for 20 days build 500 meters of a wall, how many men will it take to build 1000 meters more of this wall in 30 days?=== | + | ===c. If 20 men working for 20 days build 500 meters of a wall, how many men will it take to build 1000 meters more of this wall in 30 days?=== <!--T:33--> |
| − | ==11. Demonstrate the ability to solve problem situations involving equations:== | + | ==11. Demonstrate the ability to solve problem situations involving equations:== <!--T:34--> |
| − | ===a. I have the following choice: I buy 20 units of a product with all the money I have, or buy only 14 units of a project with all the money I have, or buy only 14 units and I still have $15.00 in change. What is the unit value of this product?=== | + | ===a. I have the following choice: I buy 20 units of a product with all the money I have, or buy only 14 units of a project with all the money I have, or buy only 14 units and I still have $15.00 in change. What is the unit value of this product?=== <!--T:35--> |
| − | ===b. What is the root of the equation 7x - 2 = -4x + 5?=== | + | ===b. What is the root of the equation 7x - 2 = -4x + 5?=== <!--T:36--> |
| − | ===c. If I add 8 to the amount of toy cars I own, I will have the same amount of cars as my brother if, of the 28 that he owns, the amount that I own is subtracted. How many toy cars do I have?=== | + | ===c. If I add 8 to the amount of toy cars I own, I will have the same amount of cars as my brother if, of the 28 that he owns, the amount that I own is subtracted. How many toy cars do I have?=== <!--T:37--> |
| − | ==References== | + | ==References== <!--T:38--> |
[[Category:Adventist Youth Honors Answer Book|{{SUBPAGENAME}}]] | [[Category:Adventist Youth Honors Answer Book|{{SUBPAGENAME}}]] | ||
<noinclude></translate></noinclude> | <noinclude></translate></noinclude> | ||
Revision as of 20:18, 7 August 2017
1. Have the Math Skills II honor.
For tips and instruction see Math Skills II.