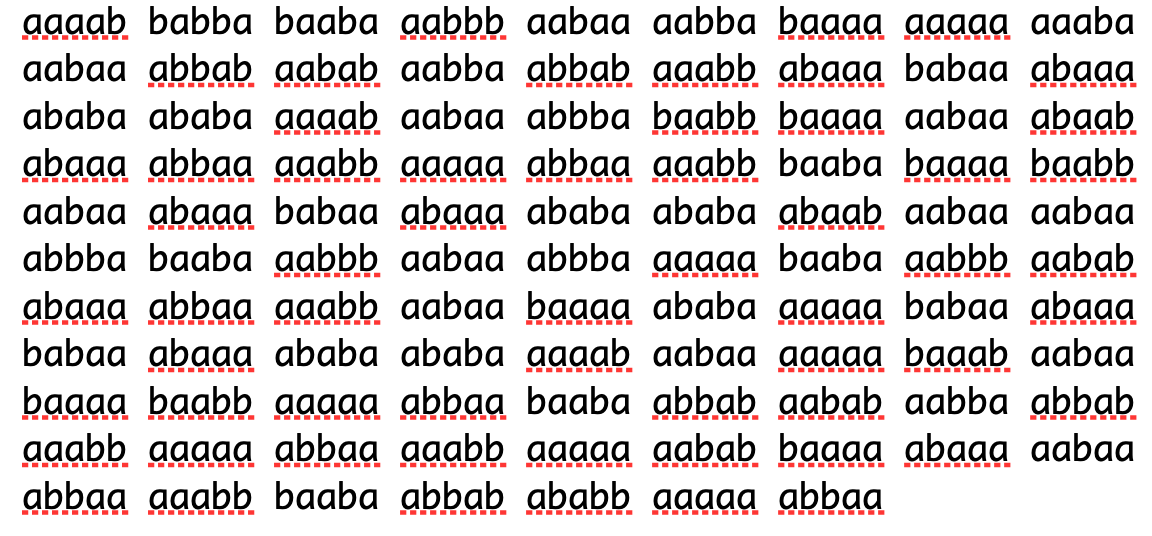Difference between revisions of "AY Honors/Cryptography/Answer Key"
| (One intermediate revision by the same user not shown) | |||
| Line 67: | Line 67: | ||
Steganography is the process of hiding data/information inside other data, for example hiding textual information in an image file, subtly changing fonts, or using invisible ink. | Steganography is the process of hiding data/information inside other data, for example hiding textual information in an image file, subtly changing fonts, or using invisible ink. | ||
| + | |||
| + | A simple two-part invisible ink can be created with things you likely already have in your house. The ink is made from a mixture of 1TBSP Baking Soda mixed in 1/2C water. Write the message with this ink on the paper. When first trying it out, use cotton swabs, but later you can experiment with finer brushes. Once the message is written, allow the paper to dry. | ||
| + | |||
| + | [[File:Ink1.jpg|frame|center|Making the Invisible Ink]] | ||
| + | [[File:Ink2.jpg|frame|center|Write the message and allow to dry]] | ||
| + | |||
| + | To reveal the invisible message, mix 1tsp turmeric with 1/2c rubbing alcohol to make the reagent. Then paint the reagent over the paper. Be careful, as it is easy to stain your fingers and the table a lovely yellow. | ||
| + | |||
| + | [[File:Ink3.jpg|frame|center|Mix the reagent.]] | ||
| + | [[File:Ink4.jpg|frame|center|Use the reagent to reveal the message]] | ||
<!--T:75--> | <!--T:75--> | ||
| Line 167: | Line 177: | ||
In the image here, we have also color coded to see. So PA = BN, TH = QC, FI = EG, ND = KR, ER = AU. We would then send the encoded message (Pathfinder) as BNQCEGKRAU | In the image here, we have also color coded to see. So PA = BN, TH = QC, FI = EG, ND = KR, ER = AU. We would then send the encoded message (Pathfinder) as BNQCEGKRAU | ||
| − | |||
<!--T:91--> | <!--T:91--> | ||
<noinclude></translate></noinclude> | <noinclude></translate></noinclude> | ||
| Line 213: | Line 222: | ||
</noinclude> | </noinclude> | ||
<!-- 4. Investigate whether each item in the list below is a code, a cipher, steganography, or a plain text message. --> | <!-- 4. Investigate whether each item in the list below is a code, a cipher, steganography, or a plain text message. --> | ||
| + | |||
| + | a. Processing done by a computer to determine if a user enters a correct password | ||
| + | |||
| + | Cipher (a mathematical formula), using one-way encryption or a hash | ||
| + | |||
| + | b. A Bible verse reference | ||
| + | |||
| + | Plain text (just an abbreviation) | ||
| + | |||
| + | c. The colors used on a traffic light to mean "Stop," "Go," or "Caution" | ||
| + | |||
| + | Code (each color having a different word meaning) | ||
| + | |||
| + | d. HTTPS:// used in a URL over the Internet | ||
| + | |||
| + | Cipher to security transfer data between two points | ||
| + | |||
| + | e. Forming a message by entering it into a grid row-by-row and reading it out column-by-column | ||
| + | |||
| + | Cipher (specifically a square cipher) | ||
| + | |||
| + | f. Invisible ink | ||
| + | |||
| + | Steganography (hiding a message in plain sight) | ||
| + | |||
| + | g. Navajo language used by the Code Talkers in World War II | ||
| + | |||
| + | Code (replacing words with words) | ||
| + | |||
| + | h. Data representation via a grid of dots (QR codes) or lines (Bar codes) | ||
| + | |||
| + | Code, though could also be used to hide additional information as a form of steganography | ||
| + | |||
| + | i. Enigma machine used in World War II | ||
| + | |||
| + | Cipher - used mathematical algorithms to encode and decode messages | ||
| + | |||
| + | j. Recording your computer password on a piece of paper | ||
| + | |||
| + | Plain Text (no encoding) | ||
| + | |||
| + | k. Signal used by Jonathan and David recounted in 1 Samuel 20:18-23 | ||
| + | |||
| + | Code (each message coupled with arrow shot encoded its particular message) | ||
<!--T:97--> | <!--T:97--> | ||
| Line 227: | Line 280: | ||
[[File:Hieroglyphs from Stela of Ity.jpg|frame|A selection of hieroglyphs from the Stela of Ity, on display at the British Museum]] | [[File:Hieroglyphs from Stela of Ity.jpg|frame|A selection of hieroglyphs from the Stela of Ity, on display at the British Museum]] | ||
[[File:Selection from Stela of Semty Junior.jpg|frame|Hieroglyphs from the stela of Semty Junior, on display at the British Museum]] | [[File:Selection from Stela of Semty Junior.jpg|frame|Hieroglyphs from the stela of Semty Junior, on display at the British Museum]] | ||
| + | |||
Egyptian hieroglyphs are not really a code or a cipher, they are a form of written language. Hieroglyphs are symbols that may be phonograms (represent a sound), Ideograms (represent a word), or determinatives (provide context for the other hieroglyphs in a message). There are three types of phonograms - unilaterals (the symbol represents a single sound), bilaterals (representing a double sound, such as “pr”), and trilaterals (representing three sounds combined, such as “mwt”). | Egyptian hieroglyphs are not really a code or a cipher, they are a form of written language. Hieroglyphs are symbols that may be phonograms (represent a sound), Ideograms (represent a word), or determinatives (provide context for the other hieroglyphs in a message). There are three types of phonograms - unilaterals (the symbol represents a single sound), bilaterals (representing a double sound, such as “pr”), and trilaterals (representing three sounds combined, such as “mwt”). | ||
Latest revision as of 00:14, 7 July 2025
1
Cryptography is the science or process of encoding and decoding messages to allow more secure transfer of information.
2
2a
Codes use symbols to replace the original message. These may include images, numbers, colors, etc. In many codes, the entire word can be represented by a symbol or another word.
For example, if we see a traffic light, each color represents a word or phrase, with a specific meaning: red=stop, amber=caution, green=go. The color denotes a word, and is thus a code. At sea, ships may use flags and pennants as part of the International Code of Signals, each flag representing a letter, number, word, or phrase.
In wartime and in secret government communications, code words may be used to obfuscate the actual meaning. During World War II, for example, the U.S. Navy used code words to represent locations or activities, so if the message was intercepted, the enemy would not know what or where they were talking about.
For example, the word "BALSA" in a message meant "Midway Island," "WOODBANK" meant "Paris, France," and "RANCID" translated to "Greenland."
2b
A Cipher encrypts a message at the level of individual or small groups of letters, rather than replacing entire words. It is created (and solved) using an algorithm. A simple classic cipher, for example, is the Caesar cipher, where the alphabet is shifted a certain number of spaces to encode and decode the message. The example below is a Caesar cipher with a key of 3 (ie each letter is shifted 3 places). The algorithm could be written as (P)+X=(C), where "P" means the plain text letter, and "C" means the new cipher text letter, and "X" is the number of spaces to shift the letter. A 3 shift Caesar cipher, as below, adds 23 places (26 letters in the alphabet -3 shifted spaces) to get us our encoding, but we "subtract" three letters from the encoded message to solve for the original.
Using this cipher, we could encode the word "Ranger" as OXKDBO, the word "Voyager" as SLVXDBO
Another simple classic cipher is the Atbash cipher, where the code is the alphabet in reverse.
Using this cipher, we could encode the word "Companion" as xlnkzmrlm, the word "Guide" as tfrwv
Ciphers can be even more complex (and often are, particularly when using machines and computers). The Enigma machine of World War II used several mechanical elements to encode via a polyalphabetic cipher, meaning that in the enciphered text, a single letter may have different unencrypted meanings, based on where it was and how the algorithm encoded it.
2c
Steganography is the process of hiding data/information inside other data, for example hiding textual information in an image file, subtly changing fonts, or using invisible ink.
A simple two-part invisible ink can be created with things you likely already have in your house. The ink is made from a mixture of 1TBSP Baking Soda mixed in 1/2C water. Write the message with this ink on the paper. When first trying it out, use cotton swabs, but later you can experiment with finer brushes. Once the message is written, allow the paper to dry.
To reveal the invisible message, mix 1tsp turmeric with 1/2c rubbing alcohol to make the reagent. Then paint the reagent over the paper. Be careful, as it is easy to stain your fingers and the table a lovely yellow.
2d
Plain Text refers to the unencrypted information prior to encoding
2e
A key is the information necessary to encrypt and decrypt a particular message. In a Caesar cipher, it is the number of letters to shift.
2f
A public key is part of a two-key encryption/decryption model, where one key is private, and another is publicly available. Public Key Cryptography is also called Asymmetric Cryptography, and is a way of transmitting secure messages via the internet/email, where even if intercepted the message cannot be decrypted.
2g
A one way function is a model of encrypting information where it is relatively easy to convert the data one way, but much more difficult to reverse the process. In some computer applications, this one way function results in a hash value, allowing secure storage of sensitive information or passwords. If someone breaks into the database, they can only recover the hash value, which obscures the original information.
3
3a
Transposition is a classic cipher that moves the position of letters in a word or phrase, rather than replacing them. At its simplest, this could involve just shifting things around (Hello Friend might be encoded as Olleh Dneirf). Other forms include a rail fence ciphers as shown below, which write the words in a zig-zag pattern and then encode across the rows.
A two-line rail fence cipher, to encode "Pathfinders Strong." Once entered into the blocks, we would then send the encoded message as "PTFNESTOGAHIDRSRN"
A three-line rail fence cipher, to encode "pathfinders strong." Once entered into the blocks, we would send the encoded message as "pfetgahidrsrntnso"
3b
A traditional Polybius Square is a 5X5 grid with the alphabet filling in the square (English alphabet needs a larger square, or combines two letters, such as I and J or U and V of C and K). Each square is then given a 2 digit code as per its column and row number.
Using the square above, we would encode the word "Pathfinder" as: "53 11 44 32 12 42 33 41 51 24"
3c
In a square cipher, the letters are placed in a grid, and encoded against another grid. A common square grid is a four square grid, made up (as the name implies) of four 5X5 grids. The upper left and lower right are a regular alphabet, the upper right and lower left may have a code word (in this case Pathfinder Strong is the code word - the code word is written in the squares first, then the grid is finished with the rest of the alphabet).
To encode a message, it is first broken into two-letter segments. So pathfinder becomes pa th fi nd er (if there were an odd number of letters, you would use an x to fill the final pair). The first letter of the pair is found in the upper left grid, the second of the pair in the lower right. To encode, move along the row from the first letter to pair up with the column of the second letter. Then for the second letter, move along its row to align with the column of the first letter.
In the image here, we have also color coded to see. So PA = BN, TH = QC, FI = EG, ND = KR, ER = AU. We would then send the encoded message (Pathfinder) as BNQCEGKRAU
3d
A substitution cipher is a simple cipher, where each letter/number is replaced by an alternate letter/number/symbol. The characters are changed for the encoded message, but not the order of characters. Morse Code can be considered a substitution cipher, as each letter is replaced with a unique set of dashes and dots, which allowed the message to be sent across telegraph lines by sending longer (dash) or shorter (dot) pulses of electricity.
3e
In a polyalphabetic cipher, the substituted letter is determined both by the key and the placement in a word. So it may be that every third letter, the cipher shifts, or there is a different cipher for first letter, second letter, third letter, etc. In this style, the encoded message letters may represent different letters in the unencoded message, as different ciphers are used for different positions. It is more complicated to decode than a simple substitution cipher.
One well known polyalphabetic cipher is the Vigenere cipher, which uses a full alphabet grid (see below).
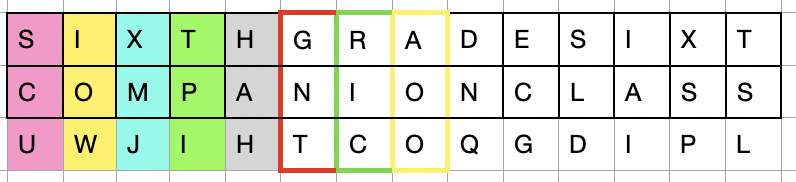
The message is encoded using a key phrase. The key phrase, repeated as necessary, is aligned above the unencoded text message, and each encoded replacement letter is found by the intersection of the key phrase letter column and the unencoded text letter row. In this case, we will use the key phrase "Sixth grade" and encode the message "Companion Class". We would align these atop one another, for example
To encode, we find the letter at the intersection of S and C, which is U. The next letter is encoded by finding the intersection of I and O, which is W. Once done, our message is encoded as UWJIHTCOQGDIPL
4
a. Processing done by a computer to determine if a user enters a correct password
Cipher (a mathematical formula), using one-way encryption or a hash
b. A Bible verse reference
Plain text (just an abbreviation)
c. The colors used on a traffic light to mean "Stop," "Go," or "Caution"
Code (each color having a different word meaning)
d. HTTPS:// used in a URL over the Internet
Cipher to security transfer data between two points
e. Forming a message by entering it into a grid row-by-row and reading it out column-by-column
Cipher (specifically a square cipher)
f. Invisible ink
Steganography (hiding a message in plain sight)
g. Navajo language used by the Code Talkers in World War II
Code (replacing words with words)
h. Data representation via a grid of dots (QR codes) or lines (Bar codes)
Code, though could also be used to hide additional information as a form of steganography
i. Enigma machine used in World War II
Cipher - used mathematical algorithms to encode and decode messages
j. Recording your computer password on a piece of paper
Plain Text (no encoding)
k. Signal used by Jonathan and David recounted in 1 Samuel 20:18-23
Code (each message coupled with arrow shot encoded its particular message)
5
a. Egyptian hieroglyphs, 1900 BC
Egyptian hieroglyphs are not really a code or a cipher, they are a form of written language. Hieroglyphs are symbols that may be phonograms (represent a sound), Ideograms (represent a word), or determinatives (provide context for the other hieroglyphs in a message). There are three types of phonograms - unilaterals (the symbol represents a single sound), bilaterals (representing a double sound, such as “pr”), and trilaterals (representing three sounds combined, such as “mwt”).
Hieroglyph words could be written right to left, left to right, top to bottom, and at times a bit of horizontal and vertical combined, depending upon how we. It fit within the physical context (thus the writing often was as much art as communication). Vowels were generally excluded (most common transliterations just toss an “e” between each consonant), and the exact pronunciation remains somewhat uncertain. Writing your name or some other message, then, may include first stripping out the vowels before encoding into hieroglyphs. You will often see people’s names enclosed in an oval, making them easier to spot. Hieroglyphs could be carved, painted, or both.
Although there were many attempts to translate hieroglyphs for centuries, the discovery of the Rosetta Stone in 1799 by the French provided the impetus for the final work to crack the “code.” The Rosetta Stone, carved around 196 BC, had the same message written in hieroglyphs (the priestly language), demotic (a more common form of written Egyptian), and ancient Greek (as Egypt had earlier been conquered by Alexander the Great). Using the Rosetta Stone as a guide, French scholar Jean-François Champollion became the first to be recognized for deciphering hieroglyphs in 1822.
Many scholars and historians of cryptology date the earliest written cipher to the tomb of Khnumhotep II, an overseer during the Middle Kingdom period of Egypt (around 1900 BC). In the tomb, located in Beni Hassan, Egypt, there are several non-standard hieroglyphs, which may have been meant to highlight key words or phrases, or make the writings appear more significant. While not necessarily meant to hide the meaning, this is often considered a first use of a substitution cipher - replacing one letter or word with another.
If you want to learn more to try and do your own hieroglyphic writing, there are several good books and online resources, including: https://www.egyptianhieroglyphs.net/ https://www.bibalex.org/learnhieroglyphs/Lesson/Introduction_En.aspx Or try an online “translator,” such as https://lingojam.com/HieroglyphicsTranslator Or try out https://artsandculture.google.com/experiment/fabricius/gwHX41Sm0N7-Dw?hl=en
b. Hebrew Atbash cipher, 500 BC
The Abash cipher is a simple substitution cipher, reversing the order of the alphabet (the name is actually the first two and last two letters of the Hebrew alphabet). Hebrew has 22 letters, and using this cipher you replace the first with last, the second with second to last, etc. If we were to use the English alphabet (26 letters), A=Z, B=Y, C=X, D=W and so on. It is a simple cipher, making it useful but easy to crack.
It is believed that there is a use of the Abash cipher in the book of Jeremiah. In Jeremiah 25:26 and 51:41, there is a mention of “Sheshach,” written right to left using the letters shin shin kaf. If an Abash cipher is applied, these would be replaced by bet bet lamed, the Hebrew word for Babel (or Babylon). Thus it is believed that here Jeremiah is referring to Babylon, not some unknown city or country of “Sheshach.” See 2b for an Abash Cipher in action
c. Julius Caesar's substitution cipher, 100 BC
The Caesar shift cipher is another simply substitution cipher and was used for military communications. The cipher “shifts” the chosen letter left or right a set number based on the cipher key. So if there is a shift 2 to the right, then the letter A in plain text is shifted to C in the cipher text - it has “shifted” 2 letters to the right.
Building a simple wheel coder/decoder is an easy way to use a Caesar cipher. It is fairly easy to break a Caesar cipher, either through brute force or (just keep replacing a letter in a word until the word makes sense) or through a frequency analysis of the coded message, recognizing that certain letters (E, T, S) are very common, and will occur more often than other letters.
See question 6 for a Caesar Cipher in action.
6
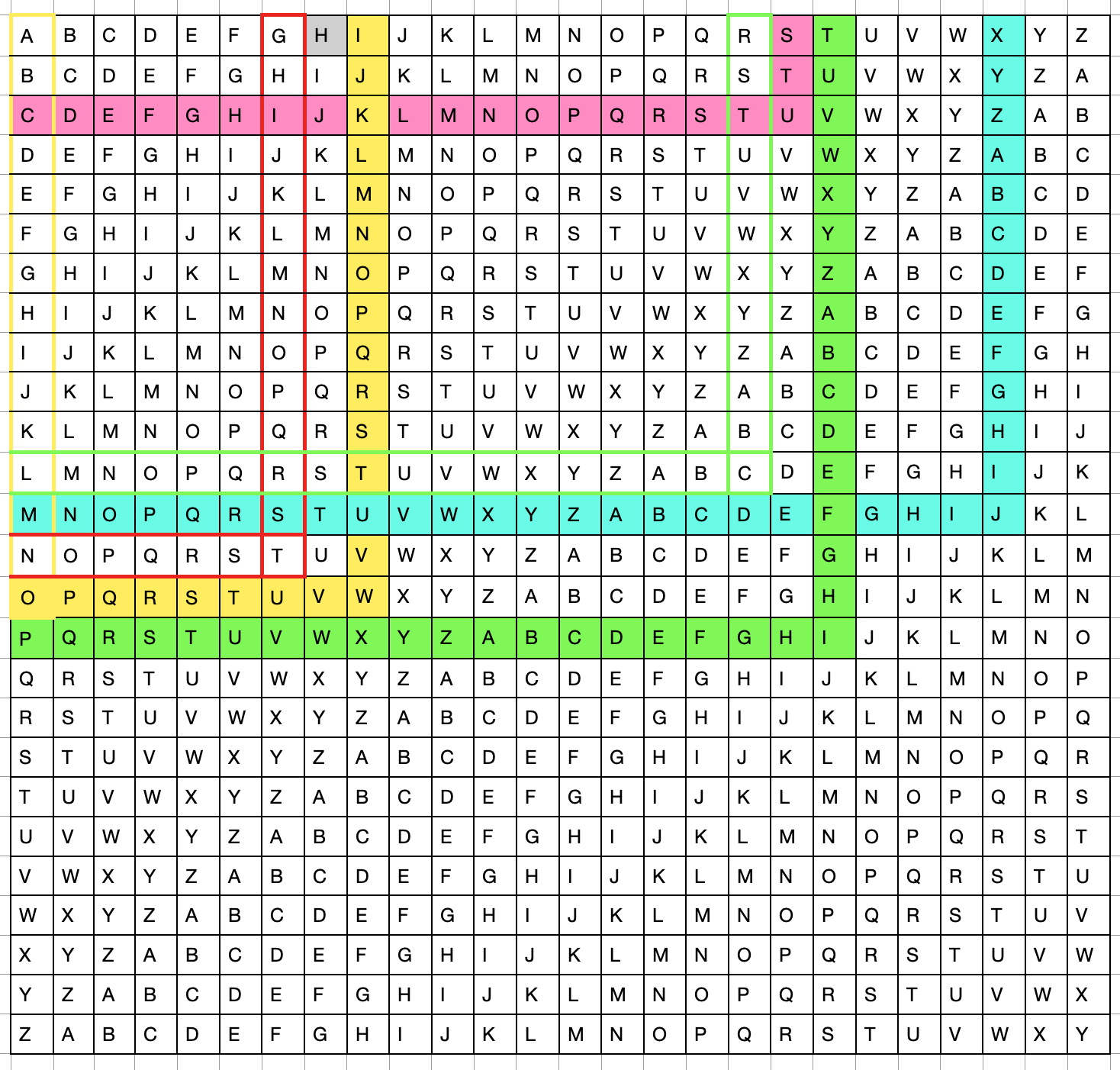
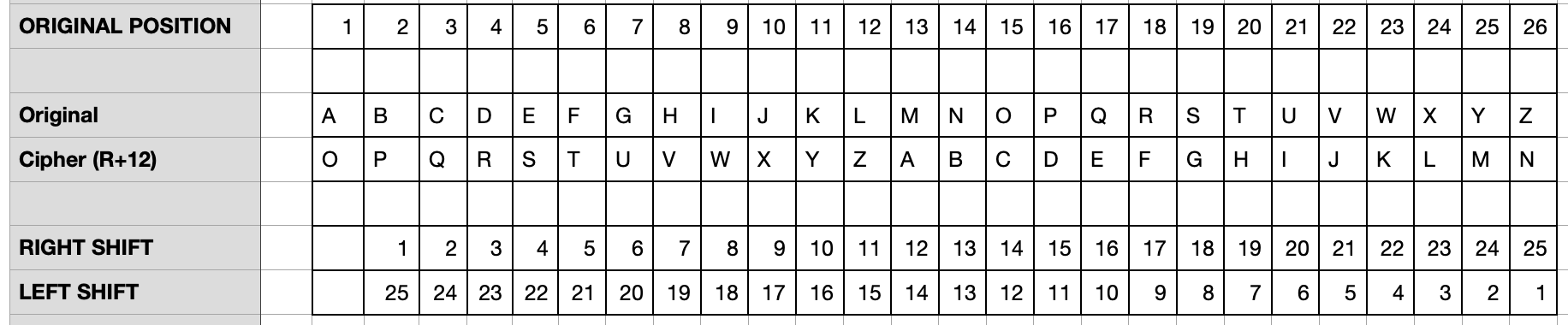
The Caesar cipher is a relatively simple cipher, with the coded text just shifting the letter a certain number of spaces left or right along the alphabet. If we have 26 letters in the alphabet, it means we can shift the alphabet 25 different ways right and 25 different ways left. A "right +2" Caesar cipher would move each letter two spaces to the right, so "A" would be encoded as "C," "B" would be "D" and so on, until "Y" wrapped around to "A" and "Z" wrapped around to be encoded as "B."
Here is a left +12 Caesar cipher (12 for the number of disciples). You can use a code phrase or some other way to signify the shift (though Caesar ciphers are relatively simple to break using brute force approaches and basic logic of language).
To use this, we first lay out our plain text
Now we encode the letters using our left +12 Caesar cipher
Finally, we remove our plain text, and can send the encoded text instead.
7
There are many online tools to embed messages in images using ‘least significant bit’ (LSB) steganography, which changes one character in the encoding of the colors for pixels. This is nearly invisible to the human eye, but can be decoded by machine. Changing a file by saving it somewhere else, or in a different format, however, may compromise the message. Information can also be hidden in video files, music files, and other digital media.
But one doesn't always need a computer to hide messages in plain sight. This has been done for centuries, by hand. Steganography is hiding a message in plain sight. One simple way to do this is to write the message in invisible ink, such as lemon juice. When the ink dries, it cannot be seen on the paper until treated (with lemon juice, that means exposing it to heat). If you write the message over an already printed paper, it is even more hidden, as those intercepting the message will think the plain text is the message when in fact the real message is hidden underneath and waits to be revealed.
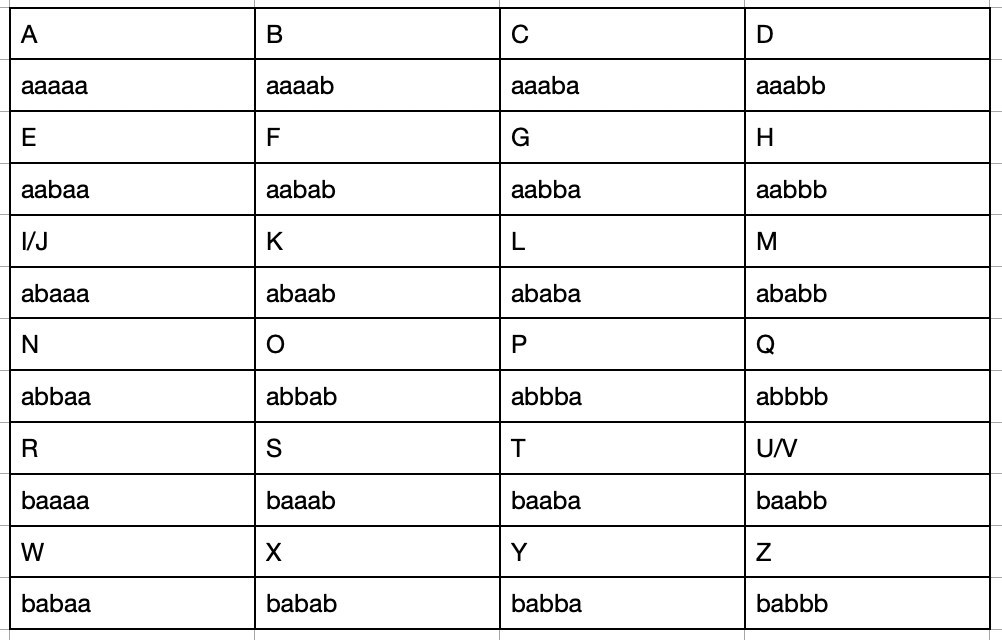
For a time-consuming but clever text based steganography, we can use Bacon's cipher to encode the Pathfinder Pledge. Bacon's cipher first replaces each letter with a five-letter a-b key (similar to binary, but using a and b rather than 0 and 1). Then, the message is written by using a different font or other clue for each a or b mapped against a piece of concealment text. It doesn't matter what the text is, so long as when it is written, one can break it into blocks of five letters, and see which letter represents an a or a b. Those five character a-b blocks then remap against the original cipher, revealing the original text.
Using Bacon's cipher, we can convert the Pathfinder Pledge to the following string of five-character a-b blocks. So we converted By (the first word of the pledge) into aaaab babba, and continue with the whole Pledge, ignoring spaces and punctuation.
Now we need our concealment text. The encrypted text is 485 characters long, so we need at least that much text. For this exercise, we have a selection from The Pathfinder Story, which, with its citation, is exactly 485 characters. We will hide the a-b encrypted text within this concealment text.
Now we take our concealment text, remove all of the punctuation and spaces, and break it into five character blocks, so we can map it against the cipher.
We can then map this set of five character text blocks against our cipher text so we know what characters to slightly alter to encode our message in plain sight.
For this version, we then take all of the letters that map against an "a" in the cipher text and leave them as 14 point font, while all the letters that map against a "b" in the cipher text are converted to 13 point font. It is a little noticeable, but not immediately obvious in the text that we have a hidden code.
To make it easier to see, here is some of the text with the 13 point font letters in red. We would not send it this way, but this may help you see how the encoding works in the concealment message.
To decrypt, we reverse the process. We first break our text into five character blocks, so we will be able to write out the cifer text. Here, we are using red to showcase which characters were in the 13 point font, while we leave the 14 point font characters in black.
Next, we convert the coded concealment text into a-b blocks. In this case, red (13 point font) letters are converted to "b," black (14 point font) characters are converted to "a."
Finally, we take the cipher text (the a-b blocks) and convert them to letters, giving us our hidden message.
The clever thing about Bacon's cipher, despite the long process, is that done right, it is almost impossible to tell that there is even a hidden message. By hiding the message in plain sight, others are less likely to think it is a message, and thus wont even work to break the cipher.
8
You have plenty of choices for this one.
Here is an example of using a columnar transposition cipher (with a key) to encode our message. In this form of cipher, we write our plain text in a grid horizontally, and write our cipher text by reading the columns vertically. But the twist is the key. Before writing our text, we write the key word across our grid. This determines how many rows we will have. The rows are then written as the cipher text based on the alphabetical order of the letters in the key word - so the first column isn't necessarily the first column we will write. If there are two of the same letter in the key word, the first appearance comes first in numbering the columns.
So here is the way to encrypt using this method. Our plain text comes from the book of Psalm. Here we have converted the numbers to words so we do not need to worry about having numbers mixed with out letters.
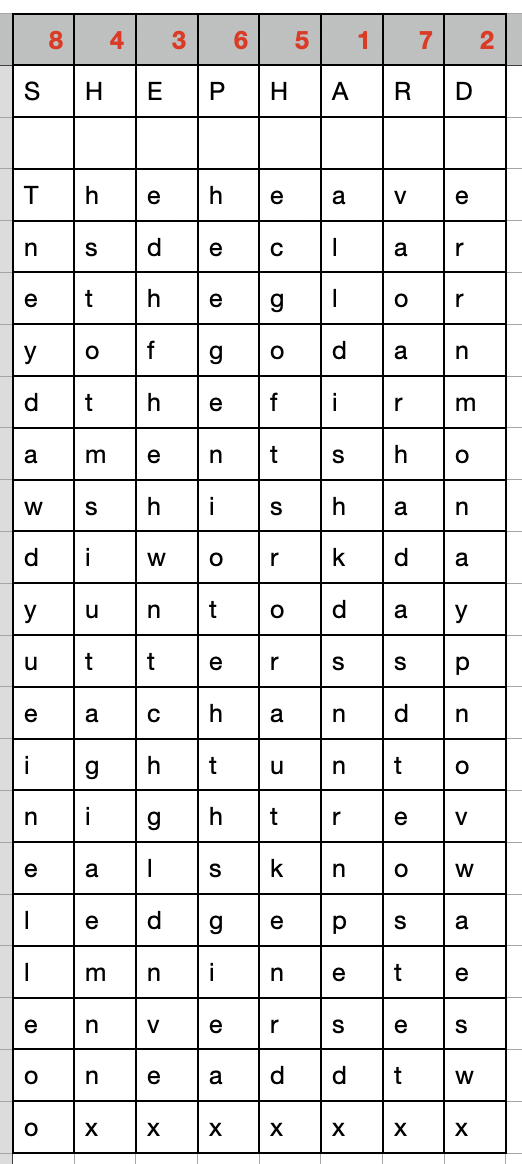
Our keyword is SHEPHARD. Yes, it is spelled like a person's name, not the job with sheep. Using similar sounding words can add to the complexity if someone overhears the key word. The keyword should be sent (or pre-arranged) separately from the cipher text. Perhaps you can use steganography to hide the key word. So, our key, shephard, has 8 letters, so we will have 8 columns in our grid. When we encode, we will begin with the column beneath the letter "A," then the column beneath the letter "d," then "e," then the first "H," then the second "H" and so on. So here is the verse written out in our grid.
Now we write out the coded message, starting with the column under "a," and so on.
Finally, we break it up (this time in groups of 5, but use whatever you want so long as it isnt the original number of columns)
To decode, we would take the key word, make a grid, count the total number of characters in the encoded message and divide by the number of columns in our table to determine how many rows we need. Then we begin writing the cipher text vertically in the table, beginning with the "A" column and so on. Once complete, we read/write it out horizontally across the rows to recover our original text.
9