Especialidades JA/Óptica/Respuestas
1
1a
1b
1c
1d
1e
1f
1g
1h
1i
2
Amazonite is an opaque green to blue-green form of feldspar.
Mirror
Light striking a mirror is reflected. The angle at which the light strikes a mirror is equal to the angle of its reflection.
3
The four lenses at the top of this illustration are positive. The four along the bottom are negative.
4
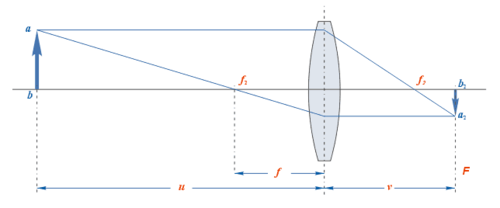
It depends on how accurately you want to measure the focal length. The focal length can be determined by the equation:
- [math]\displaystyle{ \frac{1}{u} + \frac{1}{v} = \frac{1}{f} }[/math]
Where [math]\displaystyle{ u }[/math] is the distance between the center of the lens and the light source, and [math]\displaystyle{ v }[/math] is the distance between the image the lens makes and the lens itself. If [math]\displaystyle{ u }[/math] is greater than 30 times the focal length, it can be disregarded because [math]\displaystyle{ \frac{1}{u} }[/math] is so small.
If you are using the sun for the light source, [math]\displaystyle{ u }[/math] is 93 million miles, meaning [math]\displaystyle{ \frac{1}{u} }[/math] is so tiny as to practically be zero.
5
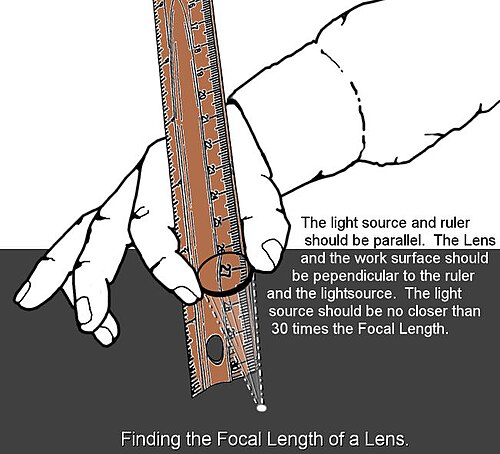
Positive Lens
Set a ruler on end on a work surface (a table, sidewalk, or a wood board). Using a bright light (such as the sun) as the light source, hold the lens against the ruler and slide it up and down the ruler until the light is focused on the work surface. The point on the ruler that the focused lens touches is to be recorded as the Focal Length for that lens.
Negative Lens
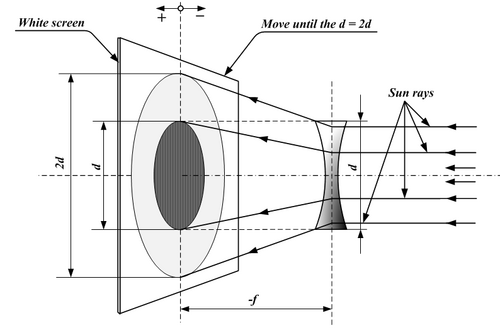
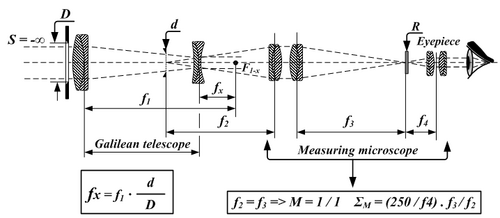
Measuring the focal length of a negative lens is more difficult because light going through it does not converge to form an image. Instead, you will need to place a positive lens between the light source and the negative lens. Move the lenses and screen around until the light is focused.
Once focused, we can measure the distance between the negative lens and the image on the screen and call it [math]\displaystyle{ v_2 }[/math]. The only other information we need for calculating the focal length of the negative lens is the distance between the negative lens and its object. But where is its object? It lies between the negative lens and the screen at the positive lens's focal point (which you have presumably already measured).
Therefore, the distance between the negative lens and its object [math]\displaystyle{ u_2 }[/math] is the distance between the lenses [math]\displaystyle{ d }[/math] minus the positive lens's focal point [math]\displaystyle{ f_1 }[/math]
- [math]\displaystyle{ u_2 = d - f_1 }[/math]
Note that [math]\displaystyle{ d }[/math] should be smaller than [math]\displaystyle{ f_1 }[/math] making [math]\displaystyle{ u_2 }[/math] a negative number.
Once we have [math]\displaystyle{ u_2 }[/math], we can get the focal length [math]\displaystyle{ f_2 }[/math]:
- [math]\displaystyle{ \frac{1}{f_2} = \frac{1}{v_2} + \frac{1}{u_2} }[/math]
[math]\displaystyle{ f_2 }[/math] should come out as a negative number.
Another method for measuring focal length of a negative lens:
6
By drawing lines representing the rays of light, we can show that the light creates an inverted image.
7
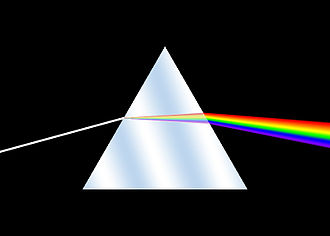
A prism uses the fact that different colors of light are bent differently as they travel through a medium. This effect is also seen in chromatic aberration.
The shape of a prism is an equilateral triangle. This causes the colors of light to disperse in a very predictable way.
8
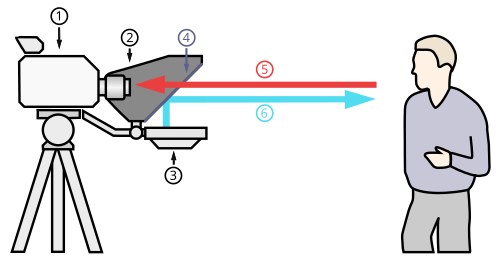
One-way glass, also called a two-way mirror, or a one-way mirror, is a pane of glass with a partially reflective, partially transparent layer, used with a darkened room on one side and a well-lit room on the other, allowing those in the darkened room to see into the lighted room but not vice versa.
The glass is coated with (or in some cases encases a layer of) a very thin almost transparent layer of metal (generally aluminum) to enhance its reflective nature. The result is what appears to be a mirror from one side, and tinted glass from the other. A viewer in the brightly lit area has difficulty seeing into the darkened room, through what appears to be a mirror.
To take full advantage of the partially mirrored surface, the target side should be brightly lit, to obscure any hint of light coming through the glass from the viewer's side. The darkened room is only completely obscured when it is in complete darkness. Sometimes a darkened curtain or a double door type vestibule is used to keep the viewers side darkened.
Uses
One-way glass is used for:
- providing security, through covert viewing, of public spaces.
- for the protection of covert camera
- for some police interrogation rooms.
- The use of one-way glass is also apparent in the broadcast television where persons read from a script while seemingly looking directly at the camera. This effect is achieved where the camera is the viewer looking through the glass, upon which the prompt or script is also reflected for the subject to read.
9
Periscope
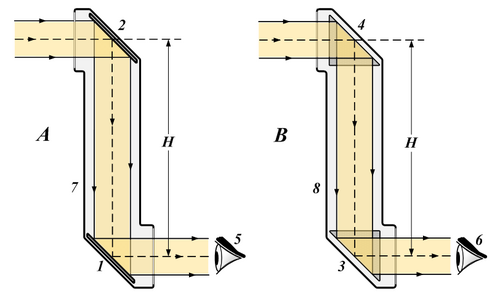
A - Periscope using two plane mirrors.
B - Periscope using two right–angled prisms.
1 - 2 - Plane mirrors.
3 - 4 - Right–angled prisms.
5 - 6 - Observer eye.
7 - 8 - Periscope tube.
H - Periscope optical height.
Different types of periscopes:
Lens periscopes. [2]
Handheld periscope. [3]
Submarine periscope.[4]
A periscope is an instrument for observation from a concealed position. In its simplest form it is a tube in each end of which are mirrors set parallel to each other and at an angle of 45° with a line between them.
A periscope may be used as a toy or for seeing over people's heads in a crowd. This form of periscope, with the addition of two simple lenses, was used for observation purposes in the trenches during World War I.
A simple periscope can be made from two small, flat mirrors and a rectangular box (such as those in which aluminum foil or wax paper are packaged). Hot melt glue and strips of cardboard can be used to hold the mirrors in place.
Slide Projector
A slide projector is an opto-mechanical device to view photographic slides. It has four main elements: a fan-cooled electric light bulb or other light source, a reflector and "condensing" lens to direct the light to the slide, a holder for the slide and a focusing lens. A flat piece of heat absorbing glass is often placed in the light path between the condensing lens and the slide, to avoid damaging the latter. This glass transmits visible wavelengths but absorbs infrared. Light passes through the transparent slide and lens, and the resulting image is enlarged and projected onto a perpendicular flat screen so the audience can view its reflection.
Opaque Projector
The opaque projector, epidioscope, epidiascope or episcope is a device which displays opaque materials by shining a bright lamp onto the object from above. A system of mirrors, prisms and/or imaging lenses is used to focus an image of the material onto a viewing screen. Because they must project the reflected light, opaque projectors require brighter bulbs and larger lenses than overhead projectors. Care must be taken that the materials are not damaged by the heat generated by the light source. Opaque projectors are not as common as the modern "overhead".
Opaque projectors are typically used to project images of book pages, drawings, mineral specimens, leaves, etc. They have been produced and marketed as artists’ enlargement tools to allow images to be transferred to surfaces such as prepared canvas, or for lectures and discourses.
Refracting Telescope
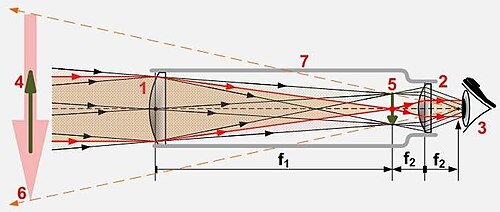
All refracting telescopes use the same principles. The combination of an objective lenses (1) and some type of eyepiece (2) is used to gathered more light than the human eye could collect on its own, focused it (5), and present the viewer with a brighter, clearer, and magnified virtual image (6). The objective in a refracting telescope refracts or bends light. This refraction causes parallel light rays to converge at a focal point; while those which were not parallel converge upon a focal plane. Refracting telescopes can come in many different configurations to correct for image orientation and types of aberration. Because the image was formed by the bending of light, or refraction, these telescopes are called refracting telescopes or refractors.
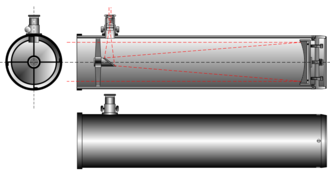
Reflecting Telescope
In this diagram, light enters the telescope tube from the left and strikes the primary mirror (which is concave). Light is then focused onto the secondary mirror mounted on a set of struts, and is then reflected out the side of the tube to the eyepiece.
10
The numbers used for describing binoculars give the power followed by the diameter of the objective lens (The largest diameter lens) in millimeters. This means that 6x35 have a magnifying power of 6x and have a diameter of 35mm.
The power represents how much bigger an object appears than with the unaided eye. You can also think of how many times closer it appears to be. The diameter lets you know how much light is gathered by the lens. A 50mm objective lens gathers much more light than a 35mm objective lens. Because the amount of light that is gathered increases if we increase the area that the light hits, we can calculate the light gathering of a lens using the area of a circle:
Area of lens= π (radius of lens)[math]\displaystyle{ ^2 }[/math]
| Binocular Specification | Magnifying Power | Diameter of objective (mm) | Area of objective [math]\displaystyle{ mm^2 }[/math] | Light gathering power (compared to unaided eye) |
| Unaided Eye | 1x | 8 | 50.265 | 1x |
| 10x25 | 10x | 25 | 490.8738 | 9.7x |
| 6x35 | 6x | 35 | 962.11275 | 19.14x |
| 7x50 | 7x | 50 | 1,963.495 | 39.06x |
The 50mm objective lens collects 2.0408... times more light than a 35mm objective lens. If you are in a dark environment, you will get twice as much light with the 7x50 binoculars than with a 6x35. The 7x50 binoculars has more magnifying power (7/6 or 1.167 times) than the 6x35 binoculars.
The higher the first number, the larger things appear, but the harder it is to hold the binoculars steady. Above 10x most people need a tripod to hold it steady enough to be useful. The higher the second number, the more light gathering power, which allows you to continue to see even in low light conditions, but the binoculars are much heavier as well.
Knowing what the numbers on a pair of binoculars mean is important as you are choosing which ones are best for you, but binoculars are a very personal thing, so try them before you buy them.
11
A faster lens has a lower f-number, and lets in more light than a slower lens. The f-number is the ratio of the diameter of the entrance pupil to the focal length of the lens.
[math]\displaystyle{ f\ number = \frac {Focal\ length} {Diameter\ of\ objective} }[/math]
The two parameters that define the f-number of an optical system are:
- Focal Length
- The longer the focal length, the more magnifying power the optical system has. You will choose a very long focal length lens if you wish to photograph birds, and a short focal length lens to photograph scenic shots such as a panarama.
- Diameter of the lens
- The larger the diameter the more light is let in. So to have a fast lens, you will need a large diameter lens, and the longer the focal length, the larger the diameter needs to be to have the same speed. A 50mm f/4 lens will have a diameter of 12.5 mm, but a 400mm f/4 lens will have a diameter of 100mm.
The advantage of a faster lens is that there is more light, so it is easier to see, and for photography, you can keep the exposure time low.
The disadvantage of a fast lens is that it is heavier, and has less depth of field.
References